
РТМ 108.038.101-77 Трубопроводы стационарных паровых и водогрейных котлов. Расчет на самокомпенсацию
РТМ 108.038.101-77
Группа Е26
РУКОВОДЯЩИЙ ТЕХНИЧЕСКИЙ МАТЕРИАЛ
ТРУБОПРОВОДЫ СТАЦИОНАРНЫХ ПАРОВЫХ
И ВОДОГРЕЙНЫХ КОТЛОВ
РАСЧЕТ НА САМОКОМПЕНСАЦИЮ
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ указанием Министерства энергетического машиностроения от 30.12.77 N ПС-002/9992
ИСПОЛНИТЕЛЬ - НПО ЦКТИ: Д.Л.Костовецкий, А.М.Рейнов, Е.А.Драч
ВВЕДЕН ВПЕРВЫЕ
Введен как рекомендуемый
Настоящий руководящий технический материал (РТМ) распространяется на трубопроводы стационарных паровых и водогрейных котлов.
РТМ устанавливает методику и требования по поверочному расчету указанных трубопроводов на самокомпенсацию температурных расширений.
РТМ может быть применен также для проверки компенсирующей способности трубопроводов, расположенных вне котла: трубопроводов турбоустановок, станционных трубопроводов энергоблоков и т.д.
РТМ разработан в соответствии с требованиями ОСТ 108.020.01-75.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Условные обозначения
|
|
- |
номинальный наружный диаметр поперечного сечения трубы, см; |
|
|
- |
внутренний диаметр трубы ( |
|
|
- |
номинальная толщина стенки трубы, см; |
|
|
- |
средний радиус поперечного сечения |
|
|
- |
радиус оси колена, см; |
|
|
- |
начальная овальность поперечного сечения трубы (отношение разности наибольшего и наименьшего наружных диаметров сечения к их полусумме), %; |
|
|
- |
площадь поперечного сечения трубы, см |
|
|
- |
экваториальный момент инерции поперечного сечения, см |
|
|
- |
момент сопротивления трубы изгибу, см |
|
|
- |
безразмерный геометрический параметр колена |
|
|
- |
безразмерный параметр внутреннего давления |
|
|
- |
расчетное давление среды, кгс/см; |
|
|
- |
температура нагрева стенки трубопровода (разность расчетной температуры и температуры стенки в холодном состоянии), °С; |
|
|
- |
осевая сила в сечении трубопровода, возникающая под действием самокомпенсации, кгс; |
|
|
- |
момент в сечении трубопровода, кгс·м; |
|
|
- |
составляющие момента в плоскостях |
|
|
- |
проекции силы на координатные оси, кгс; |
|
|
- |
координаты центра поперечного сечения трубопровода, м; |
|
|
- |
координаты упругого центра масс, м; |
|
|
- |
проекции поступательного перемещения сечения трубопровода, см; |
|
|
- |
углы поворота сечения трубопровода относительно координатных осей |
|
|
- |
проекции компенсируемого перемещения, см; |
|
|
- |
осевые моменты инерции трубопровода, м |
|
|
- |
центробежные моменты инерции трубопровода, м |
|
|
- |
статические моменты инерции трубопровода, м |
|
|
- |
действительная развернутая длина участка трубопровода, м; |
|
|
- |
приведенная длина участка трубопровода, м; |
|
|
- |
действительная длина отрезка трубопровода, м; |
|
|
- |
приведенная длина отрезка трубопровода, м; |
|
|
- |
коэффициент линейного расширения материала, 1/°С; |
|
|
- |
модуль упругости материала трубопровода при расчетной температуре, кгс/см |
|
|
- |
модуль упругости материала в холодном состоянии, кгс/см |
|
|
- |
коэффициент податливости колена при изгибе, учитывающий влияние внутреннего давления; |
|
|
- |
коэффициент интенсификации изгибных поперечных напряжений в колене; |
|
|
- |
эквивалентное напряжение в сечении трубопровода при действии самокомпенсации и давления, кгс/см |
|
|
- |
допускаемое напряжение при расчете элемента трубопровода на действие одного давления, кгс/см |
|
|
- |
допускаемая амплитуда напряжений, кгс/см |
|
|
- |
коэффициент перегрузки; |
|
|
- |
коэффициент прочности продольного сварного стыка; |
|
|
- |
коэффициент прочности поперечного сварного стыка при изгибе; |
|
|
- |
допуск на утонение стенки трубы, см; |
|
|
- |
монтажная растяжка, %; |
|
|
- |
коэффициент усреднения компенсационных напряжений; |
|
|
- |
коэффициент релаксации; |
|
|
- |
коэффициент, учитывающий отличие действительной формы искажения поперечного сечения трубы от строго овальной. |
|
Индексы: |
||
|
|
- |
концевые сечения трубопровода (участка трубопровода); |
|
|
- |
промежуточное сечение трубопровода; |
|
|
- |
номер отрезка трубопровода; |
|
|
- |
координатная ось; |
|
|
- |
ось, относительно которой происходит поворот или направлен момент. |
1.2. Содержащиеся в РТМ методики расчета предназначены для быстрой проверки компенсирующей способности трубопровода и предполагают выполнение соответствующих расчетов вручную (без использования ЭВМ).
1.3. В разделах 4 и 6 приведены методики расчета усилий и напряжений в трубопроводах простейшей структуры (неразветвленных). Получающиеся результаты расчета обладают точностью, соответствующей обычным методам решения задач строительной механики. Аналогичные, но более сложные методики расчета трубопроводов с ограничителями перемещений (с жесткими связями) и разветвленных трубопроводов приведены в рекомендуемых приложениях 1, 2, 3. Применение их целесообразно при отсутствии возможности проведения расчетов на ЭВМ.
1.4. В разделе 6 приведена методика оценочных расчетов усилий и напряжений в неразветвленных и разветвленных трубопроводах. Эта методика является достаточно простой, но дает грубо приближенные (оценочные, прикидочные) результаты. Последние имеют погрешность в сторону завышения, и оценка прочности по ним производится со значительным запасом.
1.5. Расчеты по настоящему РТМ несложных, малогабаритных трубопроводов с малым количеством промежуточных опор, с фиксированной конфигурацией, определяемой расположением оборудования, могут быть достаточными для проверки прочности на действие дополнительных нагрузок.
Оценку же прочности по настоящему РТМ трубопроводов сложной структуры, большого диаметра, крупногабаритных, допускающих выбор трассировки с минимальным запасом прочности (трубопроводы типа станционных трубопроводов энергоблоков) следует считать предварительной. Совершенствование компоновки и конструкции таких трубопроводов, выбор мест расположения и конструкции опор для них, а также окончательная оценка прочности их с учетом действия дополнительных нагрузок должны базироваться на расчетах, выполняемых на ЭВМ.
1.6. Для выполнения расчетов трубопроводов на ЭВМ рекомендуются программы ЦКТИ "Астра" (для ЭВМ ЕС) и "М-32-75" (для ЭВМ "Минск-32"). Эти программы реализуют требования РТМ 24.038.08-72 с учетом корректив, указанных в ОСТ 108.031.02-75.
1.7. Вопрос о достаточности расчета по настоящему РТМ должен решаться конструктором с учетом конкретных особенностей трубопровода.
1.8. Предусматриваются различные требования к расчетам высокотемпературных и низкотемпературных трубопроводов. К высокотемпературным относятся трубопроводы из углеродистых, низколегированных марганцовистых, хромомолибденовых, хромомолибденованадиевых сталей с расчетной температурой более 370 °С и трубопроводы из аустенитных хромоникелевых сталей с расчетной температурой более 450 °С. К низкотемпературным относятся трубопроводы, расчетная температура которых менее указанных значений.
1.9. Примеры расчетов трубопроводов по настоящему РТМ приведены в справочном приложении 4.
2. ОПРЕДЕЛЕНИЕ ВЕЛИЧИН, ВВОДИМЫХ В РАСЧЕТ
2.1. Модуль упругости материала 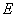 трубопровода определяется по черт.1 в зависимости от расчетной температуры стенки.
трубопровода определяется по черт.1 в зависимости от расчетной температуры стенки.
Графики модуля упругости для трубных сталей
1 - стали марок 12МХ, 15ХМ, 12Х1МФ; 2 - сталь марки 15Х1М1Ф; 3 - стали марок 15ГС, 16ГС;
4 - стали марок 3, 10, 20; 5 - сталь марки 1Х11В2МФ (ЭЦ756); 6 - стали марок 12X18H10T, 12Х18Н12Т, X14Н14B2M, Х16Н9М2
Черт.1
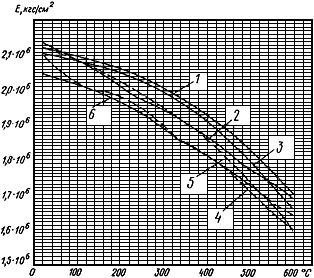
2.2. Значение коэффициента линейного расширения материала  следует принимать по черт.2.
следует принимать по черт.2.
Графики коэффициента линейного расширения трубных сталей
1 - стали марок 12Х18Н10Т, 12Х18Н12Т, Х14НВ2М, X16Н9M2; 2 - стали марок 15ГС, 16ГС; 3 - стали марок 10, 20, 3; 4 - сталь марки 12МХ; 5 - сталь марки 15ХМ; 6 - сталь марки 12Х1МФ; 7 - сталь марки 1Х11В2МФ (ЭЦ756); 8 - сталь марки 15Х1М1Ф
Черт.2
2.3. Графики для определения коэффициента усреднения компенсационных напряжений приведены на черт.3.
Графики коэффициента усреднения компенсационных напряжений для различных материалов
1 - углеродистые стали, стали марок 15ГС, 16ГС; 2 - стали марок 12Х1МФ, 15Х1М1Ф,
15ХМ, 12МХ; 3 - стали марок 12Х18Н10Т, 12Х18Н12Т, Х14Н14В2М, Х16Н9М2
Черт.3
2.4. Графики для определения коэффициента релаксации приведены на черт.4.
Графики коэффициента релаксации компенсационных напряжений для различных материалов
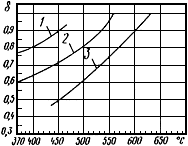
1 - углеродистые стали, стали марок 15ГС, 16ГС; 2 - стали марок 12Х1МФ, 15Х1М1Ф,
15ХМ, 12МХ; 3 - стали марок 12Х18Н10Т, 12Х18Н12Т, Х14Н14В2М, X16H9M2
Черт.4
2.5. Коэффициент податливости 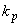 криволинейных труб и секторных колен следует определять в зависимости от параметров:
криволинейных труб и секторных колен следует определять в зависимости от параметров:
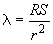 ,
, 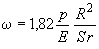
по черт.5 или по табл.1. При использовании табл.1 коэффициент 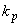 для промежуточных значений
для промежуточных значений 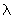 и
и 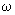 можно находить без интерполирования (берется значение
можно находить без интерполирования (берется значение 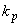 , соответствующее ближайшим значениям
, соответствующее ближайшим значениям  и
и  ).
).
Графики коэффициента
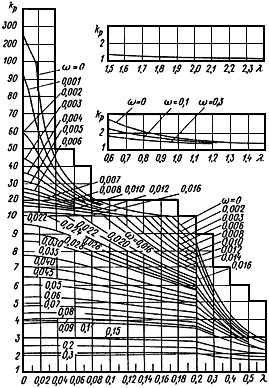
Черт.5
Таблица 1
Значения коэффициента податливости
|
|
|
|||||||||
|
0 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
0,20 |
8,68 |
7,29 |
6,23 |
5,64 |
5,11 |
4,68 |
4,34 |
4,06 |
3,82 |
3,62 |
|
0,21 |
8,26 |
7,02 |
6,14 |
5,45 |
5,00 |
4,60 |
4,27 |
4,00 |
3,77 |
3,57 |
|
0,22 |
7,88 |
6,76 |
5,96 |
5,36 |
4,89 |
4,51 |
4,20 |
3,94 |
3,72 |
3,53 |
|
0,23 |
7,54 |
6,52 |
5,78 |
5,22 |
4,78 |
4,42 |
4,13 |
3,88 |
3,67 |
3,49 |
|
0,24 |
7,22 |
6,30 |
5,62 |
5,10 |
4,68 |
4,34 |
4,06 |
3,82 |
3,62 |
3,44 |
|
0,25 |
6,92 |
6,09 |
5,45 |
4,97 |
4,58 |
4,26 |
3,99 |
3,76 |
3,57 |
3,40 |
|
0,26 |
6,65 |
5,88 |
5,31 |
4,85 |
4,48 |
4,18 |
3,92 |
3,71 |
3,52 |
3,36 |
|
0,27 |
6,39 |
5,70 |
5,16 |
4,73 |
4,39 |
4,10 |
3,86 |
3,65 |
3,47 |
3,32 |
|
0,28 |
6,16 |
5,52 |
5,01 |
4,62 |
4,30 |
4,02 |
3,79 |
3,60 |
3,42 |
3,28 |
|
0,29 |
5,94 |
5,35 |
4,89 |
4,51 |
4,21 |
3,94 |
3,73 |
3,54 |
3,38 |
3,24 |
|
0,30 |
5,73 |
5,19 |
4,76 |
4,41 |
4,12 |
3,88 |
3,67 |
3,49 |
3,33 |
3,19 |
|
0,32 |
5,35 |
4,89 |
4,51 |
4,21 |
3,95 |
3,74 |
3,55 |
3,38 |
3,24 |
3,11 |
|
0,34 |
5,01 |
4,62 |
4,30 |
4,03 |
3,80 |
3,60 |
3,43 |
3,28 |
3,15 |
3,03 |
|
0,36 |
4,71 |
4,38 |
4,20 |
3,85 |
3,65 |
3,47 |
3,32 |
3,18 |
3,06 |
2,95 |
|
0,38 |
4,44 |
4,15 |
3,91 |
3,69 |
3,51 |
3,35 |
3,21 |
3,09 |
3,00 |
2,88 |
|
0,40 |
4,20 |
3,95 |
3,73 |
3,54 |
3,38 |
3,24 |
3,11 |
3,00 |
2,90 |
2,80 |
|
0,42 |
3,98 |
3,75 |
3,58 |
3,41 |
3,26 |
3,13 |
3,02 |
2,91 |
2,82 |
2,73 |
|
0,44 |
3,79 |
3,59 |
3,43 |
3,28 |
3,14 |
3,03 |
2,92 |
2,83 |
2,74 |
2,66 |
|
0,46 |
3,61 |
3,44 |
3,29 |
3,15 |
3,04 |
2,93 |
2,84 |
2,75 |
2,67 |
2,60 |
|
0,48 |
3,44 |
3,29 |
3,16 |
3,04 |
2,94 |
2,84 |
2,75 |
2,68 |
2,60 |
2,54 |
|
0,50 |
3,29 |
3,16 |
3,04 |
2,94 |
2,84 |
2,75 |
2,68 |
2,60 |
2,54 |
2,48 |
|
0,52 |
3,16 |
3,04 |
2,93 |
2,84 |
2,75 |
2,67 |
2,60 |
2,54 |
2,47 |
2,42 |
|
0,54 |
3,03 |
2,92 |
2,83 |
2,74 |
2,67 |
2,60 |
2,53 |
2,47 |
2,42 |
2,36 |
|
0,56 |
2,91 |
2,82 |
2,74 |
2,66 |
2,59 |
2,52 |
2,46 |
2,41 |
2,36 |
2,31 |
|
0,58 |
2,81 |
2,72 |
2,65 |
2,58 |
2,51 |
2,46 |
2,40 |
2,35 |
2,30 |
2,26 |
|
0,60 |
2,71 |
2,63 |
2,56 |
2,50 |
2,44 |
2,39 |
2,34 |
2,29 |
2,25 |
2,21 |
|
0,62 |
2,62 |
2,55 |
2,49 |
2,43 |
2,38 |
2,33 |
2,28 |
2,24 |
2,20 |
2,16 |
|
0,64 |
2,53 |
2,47 |
2,41 |
2,36 |
2,32 |
2,27 |
2,23 |
2,19 |
2,16 |
2,12 |
|
0,66 |
2,45 |
2,40 |
2,35 |
2,30 |
2,26 |
2,21 |
2,18 |
2,14 |
2,11 |
2,08 |
|
0,68 |
2,38 |
2,33 |
2,28 |
2,24 |
2,20 |
2,17 |
2,13 |
2,10 |
2,07 |
2,04 |
|
0,70 |
2,32 |
2,27 |
2,22 |
2,19 |
2,15 |
2,12 |
2,09 |
2,06 |
2,03 |
2,00 |
|
0,75 |
2,17 |
2,13 |
2,10 |
2,07 |
2,04 |
2,01 |
1,98 |
1,96 |
1,93 |
1,91 |
|
0,80 |
2,04 |
2,01 |
1,99 |
1,96 |
1,94 |
1,91 |
1,89 |
1,87 |
1,85 |
1,83 |
|
0,85 |
1,93 |
1,91 |
1,89 |
1,87 |
1,85 |
1,83 |
1,81 |
1,79 |
1,78 |
1,76 |
|
0,90 |
1,84 |
1,82 |
1,80 |
1,79 |
1,77 |
1,76 |
1,74 |
1,73 |
1,71 |
1,70 |
|
0,95 |
1,76 |
1,75 |
1,73 |
1,72 |
1,70 |
1,69 |
1,68 |
1,67 |
1,65 |
1,64 |
|
1,00 |
1,69 |
1,68 |
1,67 |
1,66 |
1,65 |
1,63 |
1,62 |
1,61 |
1,60 |
1,59 |
|
1,05 |
1,63 |
1,62 |
1,61 |
1,60 |
1,59 |
1,58 |
1,57 |
1,57 |
1,55 |
1,55 |
|
1,10 |
1,58 |
1,57 |
1,56 |
1,55 |
1,55 |
1,54 |
1,53 |
1,52 |
1,52 |
1,51 |
|
1,15 |
1,53 |
1,53 |
1,52 |
1,51 |
1,50 |
1,50 |
1,49 |
1,48 |
1,48 |
1,47 |
|
1,20 |
1,49 |
1,49 |
1,48 |
1,47 |
1,47 |
1,46 |
1,46 |
1,45 |
1,45 |
1,44 |
|
1,30 |
1,42 |
1,42 |
1,41 |
1,41 |
1,40 |
1,40 |
1,40 |
1,39 |
1,39 |
1,38 |
|
1,40 |
1,37 |
1,36 |
1,36 |
1,36 |
1,35 |
1,35 |
1,35 |
1,34 |
1,34 |
1,34 |
|
1,50 |
1,32 |
1,32 |
1,31 |
1,31 |
1,31 |
1,31 |
1,31 |
1,30 |
1,30 |
1,30 |
|
1,60 |
1,28 |
1,28 |
1,28 |
1,28 |
1,27 |
1,27 |
1,27 |
1,27 |
1,27 |
1,27 |
|
1,70 |
1,25 |
1,25 |
1,25 |
1,25 |
1,25 |
1,24 |
1,24 |
1,24 |
1,24 |
1,24 |
|
1,80 |
1,23 |
1,22 |
1,22 |
1,22 |
1,22 |
1,22 |
1,22 |
1,21 |
1,21 |
1,21 |
2.5.1. Для труб, значения 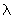 и
и 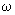 которых удовлетворяют условиям 1,6
которых удовлетворяют условиям 1,6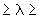 0,1 и
0,1 и 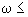 0,001, коэффициент податливости
0,001, коэффициент податливости 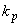 можно определять по формуле
можно определять по формуле
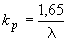 .
.
2.5.2. Для колен с 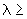 1,4 можно принимать коэффициент податливости
1,4 можно принимать коэффициент податливости 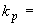 1,0.
1,0.
2.5.3. Для секторного колена в качестве величины 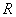 принимается радиус дуги, вписанной в многоугольник, образованный осями секторов (черт.6). Этот радиус вычисляется по формуле
принимается радиус дуги, вписанной в многоугольник, образованный осями секторов (черт.6). Этот радиус вычисляется по формуле
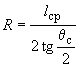 ,
,
где 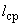 - длина сектора по центральной оси, см;
- длина сектора по центральной оси, см;
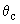 - угол между крайними сечениями сектора.
- угол между крайними сечениями сектора.
Колено, выполненное сваркой из прямых секторов (секторное колено)
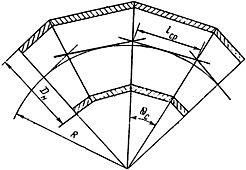
Черт.6
2.6. Коэффициент интенсификации изгибных поперечных напряжений в колене (гладком или секторном) определяется по черт.7 в зависимости от параметров 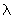 и
и 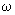 . При
. При 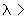 2,0 коэффициент
2,0 коэффициент 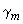 можно определять по черт.8.
можно определять по черт.8.
Графики коэффициента
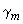
Черт.7
График коэффициента
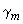
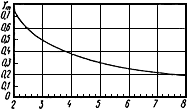
Черт.8
2.7. Если отсутствуют данные о действительной величине начальной овальности сечения колена, то значение овальности  принимается по техническим условиям или по согласованию с предприятием-изготовителем.
принимается по техническим условиям или по согласованию с предприятием-изготовителем.
Овальность колена в расчете не учитывается при 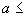 3%.
3%.
2.8. Коэффициент перегрузки 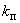 служит для учета возможного увеличения внутренних силовых факторов по сравнению с расчетными значениями. В обычных случаях можно принимать
служит для учета возможного увеличения внутренних силовых факторов по сравнению с расчетными значениями. В обычных случаях можно принимать 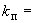 1,4. При надлежащем обосновании может быть принято более низкое значение
1,4. При надлежащем обосновании может быть принято более низкое значение 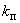 .
.
2.9. Для вычисления экваториального момента инерции поперечного сечения трубы рекомендуется формула
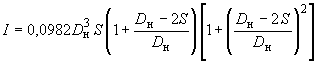 .
.
2.10. Момент сопротивления трубы изгибу вычисляется по формуле
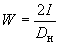 .
.
2.11. Площадь поперечного сечения трубы подсчитывается по формуле
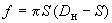 .
.
3. ОСНОВНЫЕ ПОНЯТИЯ И СООТНОШЕНИЯ
3.1. В настоящем разделе рассматривается плоский участок трубопровода, деформируемый в плоскости его осевой линии.
3.2. Если известны силы и момент, приложенные к концу  участка трубопровода, то силовые факторы в промежуточном сечении его
участка трубопровода, то силовые факторы в промежуточном сечении его  могут быть определены по формулам (решение статической задачи, черт.9):
могут быть определены по формулам (решение статической задачи, черт.9):
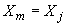 ;
;
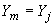 ;
;
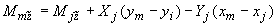 ,
,
где 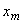 ,
, 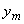 ,
, 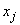 ,
, 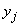 - координаты центров сечений
- координаты центров сечений  и
и  участка.
участка.
Статическая задача для трубопроводного участка
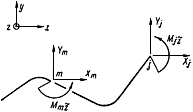
Черт.9
Полученные таким образом силовые факторы выражают действие части  участка на остальную его часть.
участка на остальную его часть.
3.3. Если  ,
,  ,
, 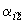 - перемещения поступательные и угловое конца
- перемещения поступательные и угловое конца  участка трубопровода, то перемещения другого конца (
участка трубопровода, то перемещения другого конца ( ) трубопроводного участка определяются формулами (решение кинематической задачи, черт.10):
) трубопроводного участка определяются формулами (решение кинематической задачи, черт.10):
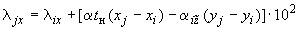 ;
;
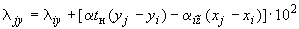 ;
;
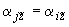 .
.
Кинематическая задача для трубопроводного участка

Черт.10
3.4. Поступательные перемещения 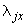 ,
, 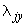 и угол поворота
и угол поворота 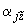 конца
конца  трубопроводного участка, вызываемые приложенными к этому концу силами
трубопроводного участка, вызываемые приложенными к этому концу силами 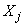 ,
, 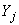 и моментом
и моментом 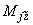 , при условии, что другой конец
, при условии, что другой конец  неподвижен, определяются формулами (решение статико-кинематической задачи, черт.11):
неподвижен, определяются формулами (решение статико-кинематической задачи, черт.11):
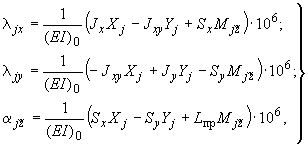 (1)
(1)
где
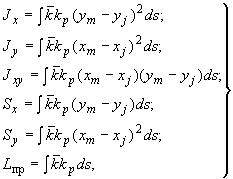 (2)
(2)
где величина 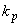 принимает значения: для прямолинейного отрезка
принимает значения: для прямолинейного отрезка 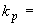 1, для криволинейного (колена) - см. п.2.5;
1, для криволинейного (колена) - см. п.2.5; 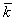 - отношение жесткости на изгиб
- отношение жесткости на изгиб 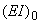 , принимаемой за эталон (например, жесткость некоторого сечения трубопроводного участка переменного диаметра) к жесткости
, принимаемой за эталон (например, жесткость некоторого сечения трубопроводного участка переменного диаметра) к жесткости 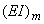 в текущей точке
в текущей точке  , т.е.
, т.е.
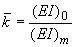 .
.
Статико-кинематическая задача
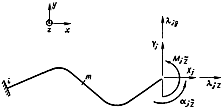
Черт.11
3.4.1. Физический смысл коэффициентов при силовых факторах в формулах (1) понятен из самих формул; эти коэффициенты характеризуют податливости участка для приложенных к его свободному концу силы и момента. По геометрическому смыслу величины 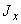 ,
, 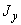 ,
, 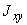 - осевые и центробежный моменты инерции трубопроводного участка относительно осей
- осевые и центробежный моменты инерции трубопроводного участка относительно осей  и
и  , проходящих через центр сечения
, проходящих через центр сечения  и направленных так же, как соответствующие оси исходной координатной системы
и направленных так же, как соответствующие оси исходной координатной системы 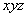 . Величины
. Величины 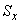 ,
, 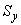 - статические моменты участка
- статические моменты участка 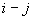 относительно тех же осей. Величина
относительно тех же осей. Величина 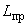 - приведенная длина участка
- приведенная длина участка 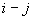 .
.
Интегрирование по формулам (2) распространяется на всю длину трубопроводного участка.
3.5. Упругий центр масс
3.5.1. Представим, что к концу  трубопроводного участка (черт.12) жестко присоединен недеформируемый (абсолютно жесткий) и ненагреваемый стержень
трубопроводного участка (черт.12) жестко присоединен недеформируемый (абсолютно жесткий) и ненагреваемый стержень  , свободный конец которого 0 располагается в центре масс фиктивных отрезков
, свободный конец которого 0 располагается в центре масс фиктивных отрезков  , распределенных по оси участка
, распределенных по оси участка  . Этот центр масс называется упругим центром масс. Статические моменты трубопроводного участка относительно проходящих через него осей равны нулю.
. Этот центр масс называется упругим центром масс. Статические моменты трубопроводного участка относительно проходящих через него осей равны нулю.
Упругий центр масс
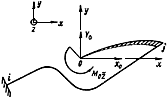
Черт.12
3.5.2. Пусть к концу 0 жесткого стержня приложены силы 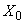 ,
, 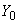 и момент
и момент 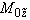 . Перемещения конца
. Перемещения конца  , вызываемые этими силовыми факторами, определяются формулами:
, вызываемые этими силовыми факторами, определяются формулами:
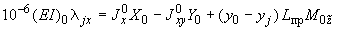 ;
;
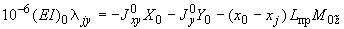 ;
;
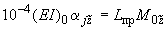 ,
,
где 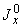 ,
, 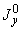 ,
, 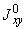 - осевые моменты инерции участка
- осевые моменты инерции участка 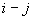 относительно осей
относительно осей  ,
,  , проходящих через упругий центр масс и направленных так же, как одноименные оси исходной координатной системы
, проходящих через упругий центр масс и направленных так же, как одноименные оси исходной координатной системы 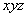 .
.
3.5.3. Использование упругого центра масс в расчетах трубопроводов дает определенные выгоды: снижается порядок системы уравнений, служащих для раскрытия статической неопределимости и облегчается построение эпюры моментов.
4. РАСЧЕТ РЕАКЦИЙ И НАПРЯЖЕНИЙ
В ПЛОСКОМ* НЕРАЗВЕТВЛЕННОМ ТРУБОПРОВОДЕ
________________
* Плоским называется трубопровод, осевая линия которого лежит в одной плоскости и деформирование которого при нагружении происходит в этой же плоскости.
4.1. Определение реактивных сил (раскрытие статической неопределимости)
4.1.1. Перемещения 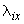 ,
, 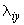 и
и 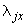 ,
, 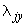 защемленных концов трубопровода ("собственные" смещения концов) и его температура нагрева считаются заданными (черт.13). Указанные перемещения положительны, если направлены в сторону положительного направления координатных осей. Принимается, что повороты концов трубопровода отсутствуют.
защемленных концов трубопровода ("собственные" смещения концов) и его температура нагрева считаются заданными (черт.13). Указанные перемещения положительны, если направлены в сторону положительного направления координатных осей. Принимается, что повороты концов трубопровода отсутствуют.
Плоский неразветвленный трубопровод
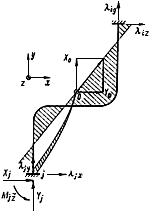
Черт.13
4.1.2. Компенсируемые перемещения определяются формулами:
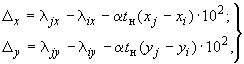 (3)
(3)
где 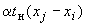 ,
, 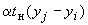 - температурные расширения трубопровода.
- температурные расширения трубопровода.
4.1.3. Уравнения, служащие для определения реактивных сил  ,
, 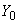 , приложенных в упругом центре масс, имеют вид (момент
, приложенных в упругом центре масс, имеют вид (момент 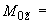 0):
0):
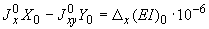 ;
;
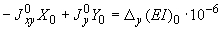 .
.
Решение этой системы записывается формулами:
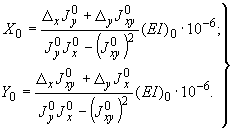 (4)
(4)
4.1.4. В высокотемпературных трубопроводах реактивные силы постепенно релаксируют. Чтобы получить значения их в рабочем состоянии трубопровода после эксплуатации в течение 10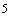 ч нужно начальные значения усилий, полученные по формулам (4), умножить на коэффициент 1
ч нужно начальные значения усилий, полученные по формулам (4), умножить на коэффициент 1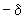 , где
, где 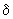 определяется согласно п.2.4. Значения реактивных сил в холодном состоянии с учетом релаксации определяются умножением начальных значений на коэффициент
определяется согласно п.2.4. Значения реактивных сил в холодном состоянии с учетом релаксации определяются умножением начальных значений на коэффициент 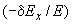 .
.
4.1.5. Монтажная растяжка в расчете реактивных усилий учитывается таким же образом, как собственные смещения защемленных концов, т.е. вместо собственных смещений в расчет вводится алгебраическая сумма их с перемещениями, соответствующими монтажной растяжке.
4.1.5.1. Если величина монтажной растяжки по осям  и
и  составляет одинаковый процент (
составляет одинаковый процент (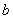 %) от величин
%) от величин 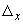 ,
, 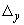 , то реактивные силы в рабочем состоянии определяются по формулам:
, то реактивные силы в рабочем состоянии определяются по формулам:
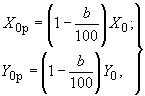 (5)
(5)
а в холодном состоянии по формулам:
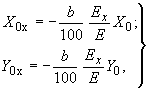 (6)
(6)
где 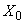 ,
, 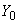 соответствуют рабочему состоянию при отсутствии монтажной растяжки (определяются по формулам (4)).
соответствуют рабочему состоянию при отсутствии монтажной растяжки (определяются по формулам (4)).
4.2. Предполагается, что в высокотемпературных трубопроводах принимается величина монтажной растяжки 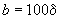 %, где
%, где 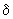 - коэффициент, определяемый согласно п.2.4.
- коэффициент, определяемый согласно п.2.4.
4.3. Построение эпюры изгибающего момента
4.3.1. Абсолютное значение изгибающего момента в некотором сечении  трубопровода определяется по формуле
трубопровода определяется по формуле
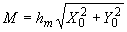 , (7)
, (7)
где 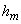 - расстояние от центра сечения
- расстояние от центра сечения  до линии действия равнодействующей сил
до линии действия равнодействующей сил 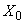 и
и 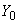 . Направление изгибающего момента устанавливается по теоретическому чертежу трубопровода (см. п.4.7.).
. Направление изгибающего момента устанавливается по теоретическому чертежу трубопровода (см. п.4.7.).
На основании формулы (7) строится эпюра изгибающих моментов (на черт.13 показана штриховкой).
4.3.2. Для колен при подсчете в них напряжений с учетом некруглости формы сечения изгибающий момент принимается положительным, когда он направлен в сторону увеличения кривизны оси колена, и отрицательным - в противном случае.
4.4. Расчет напряжений в высокотемпературном трубопроводе
4.4.1. Эквивалентное напряжение в сечении прямолинейного отрезка или колена с 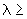 1,0 определяется по формуле
1,0 определяется по формуле
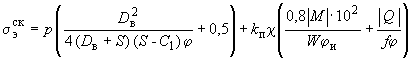 . (8)
. (8)
Коэффициенты прочности сварных стыков 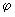 и
и 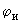 и утонение стенки
и утонение стенки 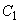 принимаются в соответствии с требованиями ОСТ 108.031.02-75. Коэффициент усреднения компенсационных напряжений
принимаются в соответствии с требованиями ОСТ 108.031.02-75. Коэффициент усреднения компенсационных напряжений 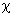 определяется согласно п.2.3. Коэффициент перегрузки
определяется согласно п.2.3. Коэффициент перегрузки 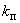 принимается согласно п.2.8.
принимается согласно п.2.8.
4.4.2. Эквивалентное напряжение в сечении колена вычисляется по формуле
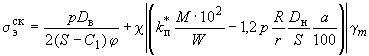 . (9)
. (9)
Коэффициент 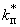 может принимать два значения:
может принимать два значения: 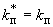 или
или 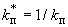 . Из них берется то значение, при котором
. Из них берется то значение, при котором 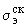 получается большим.
получается большим.
Коэффициент интенсификации изгибных поперечных напряжений 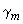 определяется в соответствии с п.2.6.
определяется в соответствии с п.2.6.
Значение овальности сечения  принимается согласно п.2.7. Расчет по формуле (9) следует производить также при
принимается согласно п.2.7. Расчет по формуле (9) следует производить также при 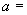 0, если действительная величина овальности сечения колена неизвестна. В случае, когда толщина стенки колена принята с учетом поправки на овальность согласно ОСТ 108.031.02-75, напряжение в колене
0, если действительная величина овальности сечения колена неизвестна. В случае, когда толщина стенки колена принята с учетом поправки на овальность согласно ОСТ 108.031.02-75, напряжение в колене 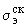 можно определять без учета овальности (
можно определять без учета овальности (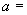 0).
0).
Для колена с 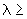 1 следует производить дополнительный расчет напряжения
1 следует производить дополнительный расчет напряжения 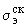 по формуле (9). Если колено имеет
по формуле (9). Если колено имеет 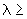 1 и
1 и 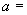 0, то расчет для него можно производить только по формуле (8).
0, то расчет для него можно производить только по формуле (8).
4.4.3. Изгибающий момент 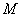 и сила
и сила 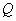 определяются без учета релаксации и монтажной растяжки трубопровода.
определяются без учета релаксации и монтажной растяжки трубопровода.
4.5. Расчет напряжений в низкотемпературном трубопроводе
4.5.1. Эквивалентное напряжение в сечении прямолинейного отрезка или колена с 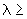 1,0 определяется по формуле
1,0 определяется по формуле
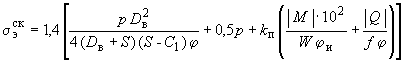 . (10)
. (10)
4.5.2. Эквивалентное напряжение в сечении колена определяется по формуле
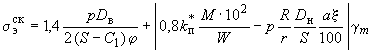 . (11)
. (11)
Величины 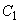 ,
, 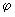 ,
, 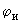 определяются согласно ОСТ 108.031.02-75. Определение
определяются согласно ОСТ 108.031.02-75. Определение 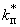 ,
, 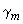 ,
,  см. п.4.4.2.
см. п.4.4.2.
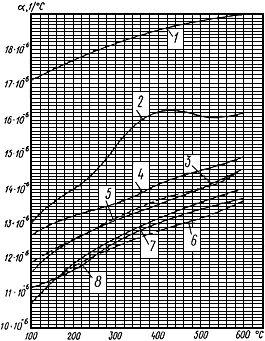
Коэффициент 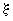 , учитывающий отличие действительной формы искажения поперечного сечения от строго овальной, принимается по графику черт.14.
, учитывающий отличие действительной формы искажения поперечного сечения от строго овальной, принимается по графику черт.14.
График коэффициента
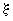
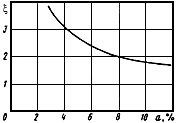
Черт.14
Если действительная величина овальности сечения колена неизвестна, то расчет напряжений в нем следует производить как при 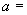 0, так и при максимально возможной величине
0, так и при максимально возможной величине  . Овальность учитывается даже в том случае, если толщина стенки колена принята по ОСТ 108.031.02-75 с учетом поправки на овальность.
. Овальность учитывается даже в том случае, если толщина стенки колена принята по ОСТ 108.031.02-75 с учетом поправки на овальность.
Для колена с 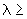 1 следует производить дополнительный расчет напряжения
1 следует производить дополнительный расчет напряжения 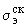 по формуле (10).
по формуле (10).
4.6. Определение перемещений промежуточных сечений
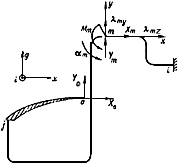
4.6.1. Температурные перемещения некоторого промежуточного сечения  трубопровода определяются по следующим формулам (черт.15):
трубопровода определяются по следующим формулам (черт.15):
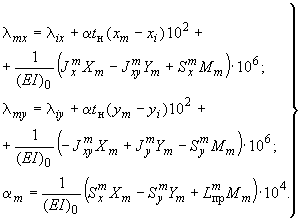 (12)
(12)
К определению перемещений промежуточного сечения трубопровода
Черт.15
Индекс  , указывающий координатную ось, относительно которой происходит поворот или направлен момент, опущен.
, указывающий координатную ось, относительно которой происходит поворот или направлен момент, опущен.
Моменты инерции 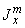 ,
, 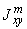 ,
, 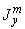 и статические моменты инерции
и статические моменты инерции 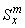 ,
, 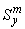 относятся к части
относятся к части 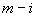 трубопровода и соответствуют осям местной координатной системы
трубопровода и соответствуют осям местной координатной системы 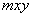 . Приведенная длина
. Приведенная длина 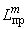 относится к части
относится к части 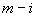 .
.
4.6.2. Силовые факторы, приложенные к концу  части
части 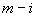 трубопровода, вычисляются по формулам:
трубопровода, вычисляются по формулам:
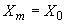 ;
;
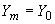 ;
;
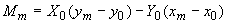 .
.
4.6.3. На черт.15 показаны силовые факторы и перемещения положительного направления. Момент и угол поворота положительны при направлении против хода часовой стрелки, если смотреть со стороны острия оси  .
.
4.7. Порядок выполнения расчета
4.7.1. В выбранном масштабе (1:100, 1:50 и т.п.) вычерчивается осевая линия трубопровода (т.е. его теоретический чертеж) и она делится на прямолинейные и криволинейные отрезки. Колена с углом между крайними сечениями более 90° делятся на два равных по длине отрезка. На теоретический чертеж наносятся центры масс отрезков. В криволинейном отрезке центр массы можно поместить на его середине. Производится нумерация отрезков: 1, 2...
4.7.2. На теоретическом чертеже трубопровода размещается исходная общая прямоугольная система координат 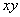 (предполагается, что ось
(предполагается, что ось  перпендикулярна плоскости чертежа и направлена острием вверх). Положение координатной системы принимается таким, чтобы облегчались дальнейшие расчетные операции. Так, следует стараться координатные оси располагать таким образом, чтобы они проходили через возможно большее число центров масс отрезков.
перпендикулярна плоскости чертежа и направлена острием вверх). Положение координатной системы принимается таким, чтобы облегчались дальнейшие расчетные операции. Так, следует стараться координатные оси располагать таким образом, чтобы они проходили через возможно большее число центров масс отрезков.
4.7.3. Определяются приведенные длины отрезков. Приведенная длина прямолинейного отрезка подсчитывается по формуле
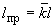 ,
,
где 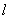 - действительная длина отрезка;
- действительная длина отрезка;
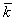 - отношение эталонной жесткости
- отношение эталонной жесткости 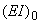 к действительной жесткости
к действительной жесткости 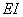 отрезка.
отрезка.
Для трубопровода, выполненного из труб одного сечения и материала, 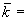 1.
1.
Приведенная длина криволинейного отрезка (колена) вычисляется по формуле
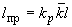 ,
,
где коэффициент податливости 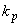 определяется согласно п.2.5.
определяется согласно п.2.5.
4.7.4. Вычисляется суммарная приведенная длина трубопровода по формуле
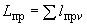 ,
,
где 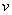 - номер отрезка трубопровода.
- номер отрезка трубопровода.
4.7.5. Непосредственными измерениями по теоретическому чертежу или подсчетами по установочным размерам определяются координаты 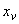 ,
, 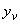 , центров масс отрезков и подсчитываются статические моменты трубопровода по формулам:
, центров масс отрезков и подсчитываются статические моменты трубопровода по формулам:
 ;
;
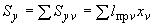 .
.
Вычисляются координаты упругого центра масс по формулам:
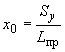 ;
;
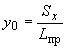 .
.
4.7.6. Определяются моменты инерции трубопровода относительно осей  ,
,  исходной координатной системы по формулам:
исходной координатной системы по формулам:
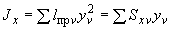 ;
;
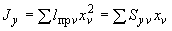 ;
;
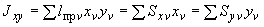 .
.
4.7.7. Определяются моменты инерции трубопровода относительно центральных осей  ,
,  ; эти оси проходят через упругий центр масс и направлены так же, как одноименные оси исходной общей координатной системы. При этом вычисления выполняются по формулам приведения:
; эти оси проходят через упругий центр масс и направлены так же, как одноименные оси исходной общей координатной системы. При этом вычисления выполняются по формулам приведения:
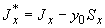 ;
;
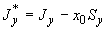 ;
;
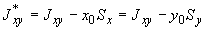 .
.
4.7.8. Вычисляются собственные моменты инерции отрезков (под собственными моментами инерции отрезка понимаются моменты инерции его относительно местных осей 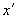 ,
, 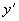 , проходящих через центр масс отрезка и направленных так же, как оси
, проходящих через центр масс отрезка и направленных так же, как оси  ,
,  общей координатной системы). Собственные моменты инерции прямолинейного отрезка вычисляются по формулам (черт.16):
общей координатной системы). Собственные моменты инерции прямолинейного отрезка вычисляются по формулам (черт.16):
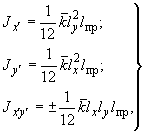 (13)
(13)
где 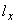 ,
, 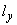 - проекции отрезка на координатные оси.
- проекции отрезка на координатные оси.
К определению собственных моментов инерции отрезка
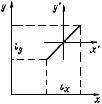
Черт.16
Если отрезок лежит в первом-третьем квадранте системы  (как на черт.16), то значение
(как на черт.16), то значение 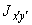 для него положительно, а если во втором-четвертом, то отрицательно.
для него положительно, а если во втором-четвертом, то отрицательно.
Для криволинейного отрезка собственные моменты инерции можно определять по формулам (13), принимая в качестве величин 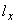 ,
, 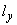 проекции хорды.
проекции хорды.
4.7.9. Вычисляются моменты инерции трубопровода относительно центральных осей с учетом собственных моментов инерции отрезков. Для этого используются следующие формулы:
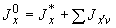 ;
;
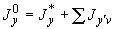 ;
;
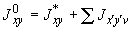 .
.
4.7.10. Один конец трубопровода обозначается буквой  , а другой (мысленно освобождаемый и присоединяемый к жесткому стержню) - буквой
, а другой (мысленно освобождаемый и присоединяемый к жесткому стержню) - буквой  .
.
По формулам (3) определяются компенсируемые перемещения. Затем по формулам (4) вычисляются реактивные силы 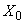 ,
, 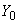 , приложенные в упругом центре масс, на конце воображаемого жесткого стержня (или к концу
, приложенные в упругом центре масс, на конце воображаемого жесткого стержня (или к концу  трубопровода).
трубопровода).
4.7.11. На теоретическом чертеже трубопровода строится эпюра изгибающих моментов: наносится его упругий центр масс и проводится через него линия действия равнодействующей сил 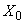 ,
, 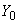 . С помощью эпюры изгибающих моментов выявляются наиболее напряженные сечения трубопровода и определяются реактивные моменты на его концах.
. С помощью эпюры изгибающих моментов выявляются наиболее напряженные сечения трубопровода и определяются реактивные моменты на его концах.
4.7.12. Подсчитываются эквивалентные напряжения в наиболее напряженных сечениях прямолинейных труб и колен трубопровода и производится оценка прочности его. Определяются реакции с учетом монтажной растяжки или саморастяжки (релаксации) - см. пп.4.1.4 и 4.1.5.
4.7.13. При необходимости вычисляются перемещения промежуточных сечений трубопровода - см. формулы (12).
4.7.14. Подсчет геометрических характеристик трубопровода удобно производить на специальном бланке (табл.2). Расположение вычислений на бланке поясняется соответствующими надписями и обозначениями.
Таблица 2
Расчет геометрических характеристик плоского трубопровода
|
Номер отрезка ( |
Приве- |
Коорди- |
Статические моменты, м |
Моменты инерции, м |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Примечание. |
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
||||||
4.7.15. Допускается исключение из расчета трубопровода некоторых его отрезков. Это эквивалентно принятию допущения о их абсолютной жесткости и дает погрешность, идущую, как правило, в безопасную сторону. В первую очередь исключаются отрезки, имеющие небольшую приведенную длину и расположенные вблизи упругого центра масс трубопровода.
4.7.16. Допускается пренебречь собственными моментами инерции некоторых отрезков (получающаяся погрешность направлена в безопасную сторону). В ходе выполнения расчета трубопровода обычно легко решается вопрос о том, собственными моментами инерции каких отрезков можно пренебречь.
5. РАСЧЕТ РЕАКЦИЙ И НАПРЯЖЕНИЙ
В НЕРАЗВЕТВЛЕННОМ ПРОСТРАНСТВЕННОМ ТРУБОПРОВОДЕ
5.1. Основные допущения и принципы
5.1.1. Каждый реактивный силовой фактор, действующий на трубопровод, вызывает деформирование его только в плоскости действия этого фактора.
5.1.2. Деформирование трубопровода рассматривается независимо в трех координатных плоскостях  ,
,  ,
,  (плоскость обозначается той же буквой, что и перпендикулярная к ней координатная ось).
(плоскость обозначается той же буквой, что и перпендикулярная к ней координатная ось).
5.1.3. Приведенные длины отрезков (прямолинейного, криволинейного) для всех трех проекций трубопровода на координатные плоскости равны. Поэтому приведенные длины трубопровода для всех трех проекций одинаковы, т.е.
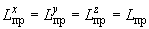 ,
,
а одноименные координаты упругого центра масс трубопровода во всех проекциях совпадают, т.е.
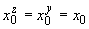 ;
;
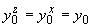 ;
;
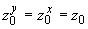 .
.
5.1.4. Для защемленных концов принимается условие отсутствия поворотов, т.е.
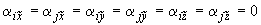 .
.
5.2. Определение реактивных сил (раскрытие статической неопределимости)
5.2.1. В общем случае неразветвленный пространственный трубопровод, не имеющий промежуточных опор, шесть раз статически неопределим; лишними неизвестными являются три силы и три момента в защемленном конце (черт.17). Однако, использование способа упругого центра масс позволяет снизить количество лишних неизвестных, определяемых из разрешающей системы уравнений, до трех. Этими неизвестными являются силы  ,
,  ,
,  , приложенные в упругом центре масс (к концу воображаемого жесткого ненагреваемого стержня, присоединенного к концу
, приложенные в упругом центре масс (к концу воображаемого жесткого ненагреваемого стержня, присоединенного к концу  ) и эквивалентные по воздействию на трубопровод реактивным силам и моментам, приложенным к концу
) и эквивалентные по воздействию на трубопровод реактивным силам и моментам, приложенным к концу  .
.
Пространственный неразветвленный трубопровод
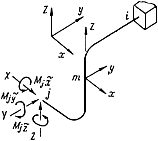
Черт.17
5.2.2. Для определения реактивных сил 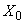 ,
, 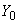 ,
, 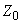 служит система уравнений:
служит система уравнений:
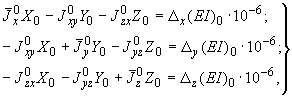 (14)
(14)
где 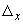 ,
, 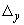 ,
, 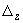 - компенсируемые перемещения (см. п.5.2.3);
- компенсируемые перемещения (см. п.5.2.3);
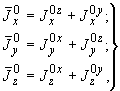 (15)
(15)
где верхний буквенный индекс указывает плоскость, в которой определяется момент инерции трубопровода.
5.2.3. Вычисление компенсируемых перемещений производится по формулам:
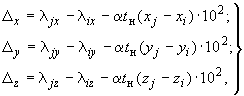 (16)
(16)
где 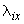 ,
, 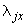 ,
, 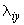 ,
, 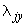 ,
, 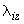 ,
, 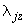 - собственные смещения защемленных концов.
- собственные смещения защемленных концов.
5.2.4. Определение реактивных силовых факторов в высокотемпературном трубопроводе с учетом релаксации производится таким же образом, как в плоском трубопроводе (п.4.1.4): умножением начальных значений на коэффициент 1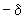 при определении реакций в горячем состоянии и на коэффициент
при определении реакций в горячем состоянии и на коэффициент 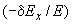 при определении их в холодном состоянии.
при определении их в холодном состоянии.
Монтажная растяжка учитывается при определении реакций так же, как в плоском трубопроводе (пп.4.1.5, 4.2).
5.3. Расчет напряжений
5.3.1. Формулы, служащие для подсчета эквивалентных напряжений в пространственном трубопроводе, аналогичны формулам (8)-(11) для определения напряжений в плоском трубопроводе. В пп.5.3.1.1 и 5.3.1.2 приводятся коррективы, необходимые при применении этих формул для расчета пространственного трубопровода.
5.3.1.1. В пространственном трубопроводе момент в поперечном сечении определяется по формуле
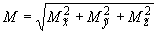
и считается величиной положительной. Здесь 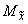 ,
, 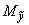 ,
, 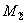 - составляющие момента, действующие в плоскостях
- составляющие момента, действующие в плоскостях  ,
,  ,
,  соответственно и определяемые по эпюрам моментов.
соответственно и определяемые по эпюрам моментов.
5.3.1.2. В формулах (9) и (11) для определения эквивалентного напряжения в колене знак минус перед слагаемым, учитывающим овальность сечения, заменяется на знак плюс и вместо 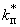 во всех случаях принимается
во всех случаях принимается 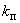 .
.
5.4. Определение перемещений промежуточных сечений
5.4.1. Поступательные температурные перемещения некоторого промежуточного сечения  трубопровода определяются по формулам:
трубопровода определяются по формулам:
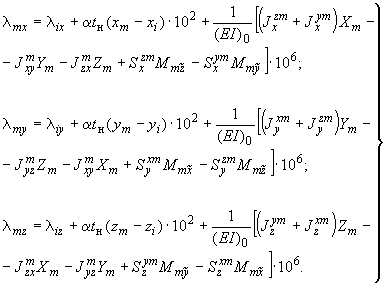 (17)
(17)
5.4.2. Угловые перемещения вычисляются по формулам:
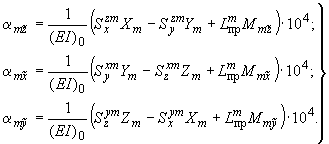 (18)
(18)
5.4.3. Моменты инерции 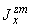 ,
, 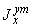 ... и т.д. и статические моменты
... и т.д. и статические моменты 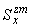 ,
, 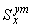 и т.д. относятся к местной системе координат
и т.д. относятся к местной системе координат 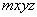 и части
и части 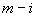 трубопровода (см. черт.17). Следует учитывать равенства:
трубопровода (см. черт.17). Следует учитывать равенства:
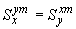 ,
, 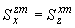 ,
, 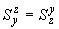 .
.
Верхние индексы  ,
,  ,
,  отмечают плоскость проекции, в которой подсчитывается данная величина. Например, величина
отмечают плоскость проекции, в которой подсчитывается данная величина. Например, величина 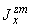 есть момент инерции относительно оси
есть момент инерции относительно оси 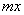 проекции на плоскость
проекции на плоскость 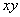 части
части 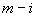 трубопровода (при замене натуральной длины отрезков приведенной длиной).
трубопровода (при замене натуральной длины отрезков приведенной длиной).
5.4.4. Силовые факторы, приложенные к концу  части
части 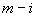 трубопровода, вычисляются по формулам:
трубопровода, вычисляются по формулам:
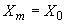 ;
;
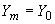 ;
;
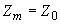 ;
;
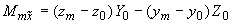 ;
;
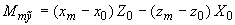 ;
;
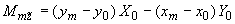 ,
,
где 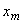 ,
, 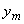 ,
, 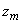 и
и 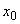 ,
, 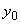 ,
, 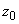 - координаты центра сечения
- координаты центра сечения  и упругого центра масс трубопровода в общей исходной координатной системе.
и упругого центра масс трубопровода в общей исходной координатной системе.
5.4.5. Положительное направление силовых факторов и перемещений определяется аналогично плоскому трубопроводу (п.4.6.3).
5.5. Порядок выполнения расчета
5.5.1. Вычерчивается теоретический чертеж трубопровода (т.е. его осевая линия): в выбранном масштабе он изображается в проекциях на три плоскости принятой прямоугольной координатной системы 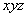 . Эта координатная система должна быть правосторонней; размещение ее следует подчинять удобству последующих расчетных операций.
. Эта координатная система должна быть правосторонней; размещение ее следует подчинять удобству последующих расчетных операций.
5.5.2. Линия трубопровода делится на отрезки (прямолинейные, криволинейные). Колено с углом более 90° делится на два равных по длине отрезка. Вычисляются приведенные длины отрезков. При этом применяются те же формулы, что и для плоского трубопровода (п.4.7.3). Производится нумерация отрезков трубопровода на всех его трех проекциях. Там же наносятся центры масс отрезков.
Таблица 3
Расчет геометрических характеристик пространственного трубопровода
|
Но- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)·(6), м |
(4)·(7), м |
(5)·(8), м |
(4)·(6), м |
(5)·(7), м |
(5)·(6), м |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Примечание. |
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
5.5.3. Измерениями по чертежу или подсчетом по проектным размерам определяются координаты 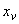 ,
, 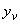 ,
, 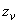 центров масс отрезков. По тем же формулам, как в случае плоского трубопровода (пп.4.7.5-4.7.9), вычисляются статические моменты, координаты упругого центра масс и центральные моменты инерции для всех трех проекций трубопровода.
центров масс отрезков. По тем же формулам, как в случае плоского трубопровода (пп.4.7.5-4.7.9), вычисляются статические моменты, координаты упругого центра масс и центральные моменты инерции для всех трех проекций трубопровода.
5.5.4. По формулам (15) вычисляются суммарные моменты инерции: 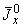 ,
, 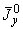 ,
, 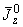 .
.
5.5.5. Один конец трубопровода обозначается буквой  , а другой (мысленно освобождаемый от наложенных связей, для которого определяются реактивные силы) - буквой
, а другой (мысленно освобождаемый от наложенных связей, для которого определяются реактивные силы) - буквой  . По формулам (16) подсчитываются компенсируемые перемещения. Решением системы уравнений (14) определяются реактивные силы
. По формулам (16) подсчитываются компенсируемые перемещения. Решением системы уравнений (14) определяются реактивные силы 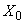 ,
, 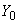 ,
, 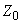 , приложенные в упругом центре масс трубопровода (они же равны реактивным силам заделки
, приложенные в упругом центре масс трубопровода (они же равны реактивным силам заделки  ).
).
5.5.6. На каждом чертеже проекций трубопровода наносится упругий центр масс и проводится линия действия равнодействующей приложенных к нему сил, лежащих в данной координатной плоскости, и так же, как в плоском трубопроводе, строится эпюра моментов.
5.5.7. Выявляются наиболее нагруженные сечения прямолинейных и криволинейных отрезков трубопровода. Для этих сечений подсчитываются эквивалентные напряжения.
5.5.8. Подсчет геометрических характеристик трубопровода удобно производить на специальном бланке (табл.3), содержащем необходимые пояснения по размещению числового материала.
5.5.9. Приведенные в пп.4.7.15, 4.7.16 замечания относительно возможности упрощения расчета плоского трубопровода могут быть распространены на пространственный трубопровод.
6. ОЦЕНОЧНЫЕ РАСЧЕТЫ ТРУБОПРОВОДОВ
6.1. Неразветвленный плоский или пространственный трубопровод
6.1.1. Предполагается, что диаметр и толщина стенки трубопровода по длине его не изменяются. Предполагается также отсутствие монтажной растяжки трубопровода и жестких связей в его промежуточных точках.
6.1.2. Равнодействующая 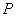 реактивных сил, возникающих в защемленном конце трубопровода, определяется по формуле
реактивных сил, возникающих в защемленном конце трубопровода, определяется по формуле
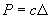 , (19)
, (19)
где 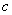 - жесткость трубопровода, кгс/см;
- жесткость трубопровода, кгс/см;
 - компенсируемое перемещение, см.
- компенсируемое перемещение, см.
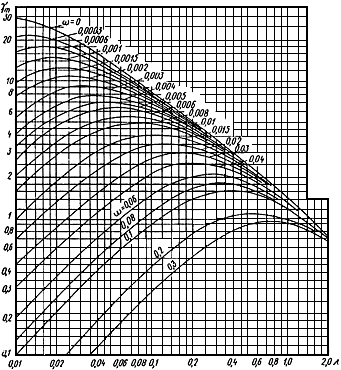
Жесткость 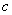 вычисляется по формуле
вычисляется по формуле
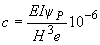 , кгс/см, (20)
, кгс/см, (20)
где 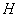 - расстояние между концами трубопровода (черт.18), м;
- расстояние между концами трубопровода (черт.18), м;
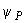 - коэффициент, определяемый по графику черт.19 в зависимости от отношения
- коэффициент, определяемый по графику черт.19 в зависимости от отношения 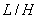 (
(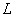 - действительная развернутая длина трубопровода, м);
- действительная развернутая длина трубопровода, м);
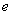 - отношение приведенной длины трубопровода (см. пп.3.4, 4.7.3, 5.5.2) к его действительной длине, т.е.
- отношение приведенной длины трубопровода (см. пп.3.4, 4.7.3, 5.5.2) к его действительной длине, т.е.
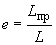 .
.
Трубопровод с обозначением размеров
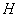 и
и
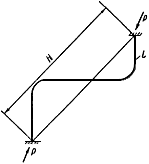
Черт.18
График коэффициента
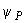
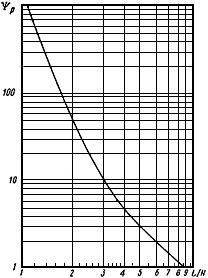
Черт.19
Если все колена трубопровода имеют одинаковое значение геометрического коэффициента 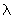 , то величину
, то величину 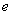 можно вычислять по формуле
можно вычислять по формуле
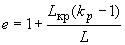 , (21)
, (21)
где 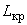 - часть действительной длины трубопровода, приходящаяся на все его колена, м;
- часть действительной длины трубопровода, приходящаяся на все его колена, м;
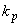 - коэффициент податливости колена (определение его см. п.2.5).
- коэффициент податливости колена (определение его см. п.2.5).
6.1.3. Компенсируемое перемещение  определяется по формуле
определяется по формуле
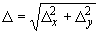 (22)
(22)
для плоского трубопровода и по формуле
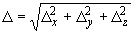 (23)
(23)
для пространственного трубопровода.
Компоненты перемещения 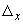 ,
, 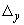 ,
, 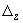 вычисляются по формулам (3) для плоского трубопровода или (16) для пространственного трубопровода.
вычисляются по формулам (3) для плоского трубопровода или (16) для пространственного трубопровода.
6.1.4. Максимальные эквивалентные напряжения самокомпенсации в высокотемпературном трубопроводе определяются по следующим формулам:
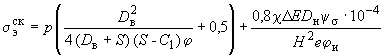 (24)
(24)
для прямолинейной трубы;
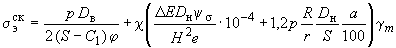 (25)
(25)
для колена,
где 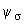 - коэффициент, принимаемый по черт.20.
- коэффициент, принимаемый по черт.20.
График коэффициента
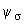
Черт.20
При 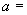 0 и
0 и 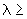 1,0 расчет эквивалентного напряжения в колене производится по формуле (24).
1,0 расчет эквивалентного напряжения в колене производится по формуле (24).
Определение величин 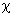 ,
, 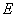 ,
, 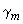 ,
,  дано в разделе 2. Овальность сечения колена не учитывается (
дано в разделе 2. Овальность сечения колена не учитывается (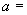 0), если толщина стенки его принята в соответствии с ОСТ 108.031.02-75. Значения
0), если толщина стенки его принята в соответствии с ОСТ 108.031.02-75. Значения 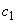 ,
, 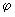 ,
, 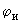 принимаются по ОСТ 108.031.02-75.
принимаются по ОСТ 108.031.02-75.
6.1.5. Максимальные эквивалентные напряжения самокомпенсации в низкотемпературном трубопроводе определяются по формулам:
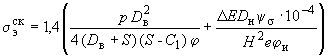 (26)
(26)
для прямолинейных труб;
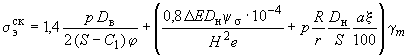 (27)
(27)
для колен.
Определение 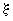 см. п.4.5.2.
см. п.4.5.2.
6.2. Разветвленный трубопровод
6.2.1. Изложенная в п.6.2 методика относится к разветвленному трубопроводу с одним узлом (черт.21).
Разветвленный трубопровод с одним узлом
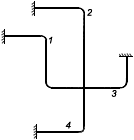
1, 2, 3, 4 - участки трубопровода
Черт.21
6.2.2. Трубопровод расчленяется на участки (см. п.1 рекомендуемого приложения 2), и каждый участок рассчитывается по изложенной в п.6.1 методике как неразветвленный трубопровод с подсчитанным согласно п.6.2.3 компенсируемым перемещением  .
.
6.2.3. Компенсируемое перемещение  некоторого
некоторого  -го участка трубопровода определяется по формуле
-го участка трубопровода определяется по формуле
 ,
,
где 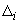 - перемещение, вычисляемое по формуле (22) для плоского трубопровода или по формуле (23) для пространственного трубопровода при условии неподвижности узла трубопровода;
- перемещение, вычисляемое по формуле (22) для плоского трубопровода или по формуле (23) для пространственного трубопровода при условии неподвижности узла трубопровода;
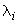 - смещение узла трубопровода, определяемое по формуле
- смещение узла трубопровода, определяемое по формуле
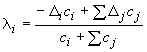 , (28)
, (28)
где 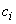 - жесткость
- жесткость  -го участка, определяется по формуле (20);
-го участка, определяется по формуле (20);
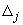 ,
, 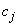 - перемещение и жесткость
- перемещение и жесткость  -го участка.
-го участка.
Суммирование по формуле (28) распространяется на все участки трубопровода, за исключением  -го участка.
-го участка.
6.2.4. Реактивная сила, возникающая в  -ом участке, определяется по формуле
-ом участке, определяется по формуле
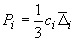 . (29)
. (29)
6.2.5. Напряжения вычисляются с использованием формул (24)-(27), но коэффициент 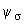 берется с уменьшением в 2,5 раза.
берется с уменьшением в 2,5 раза.
6.2.6. Расчет по пп.6.2.4 и 6.2.5 производится для каждого участка трубопровода.
6.2.7. Как правило, приведенная в п.6.2 методика дает значения реактивной силы и напряжений со значительным завышением (иногда в 5 и более раз).
7. РАСЧЕТ НАПРЯЖЕНИЙ В ТРУБАХ ТРУБНОГО ПАКЕТА КОЛЛЕКТОРА КОТЛА
7.1. В некоторых конструкциях котлов поверхности нагрева присоединяются к пароотводящему коллектору с помощью множества коротких труб (пакетов, лент) (черт.22).
Трубный пакет коллектора и нагрузки, воздействующие на коллектор
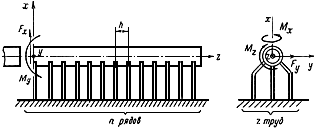
Черт.22
Коллектор одним своим концом присоединяется к станционному паропроводу, составляя его продолжение. Приводимая в настоящем разделе методика расчета труб пакетов является приближенной, включающей ряд упрощающих допущений. В частности, пакет труб схематизируется сплошным упругим основанием.
7.2. Внутренние силовые факторы в сечении коллектора в месте присоединения первого крайнего ряда труб пакета (со стороны станционного паропровода) определяются расчетом паропровода на ЭВМ при условии абсолютной жесткости пакета. Эти силовые факторы при положительном их направлении показаны на черт.22.
7.3. Наиболее напряженными являются трубы крайних рядов пакета. Нагрузки, действующие на трубу первого ряда, определяются формулами (см. черт.23, где изображены силы положительного направления):
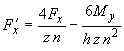 ;
; 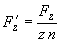 ;
;
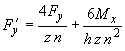 ;
; 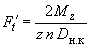 .
.
Труба крайнего ряда пакета с приложенными нагрузками
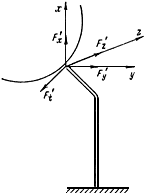
Черт.23
Силы, воздействующие на трубу последнего ряда, определяются по следующим формулам (черт.22):
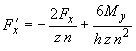 ;
; 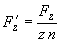 ;
;
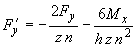 ;
; 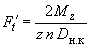 ,
,
где  - число труб в одном ряду (перпендикулярном оси коллектора) пакета;
- число труб в одном ряду (перпендикулярном оси коллектора) пакета;
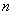 - число рядов труб в пакете;
- число рядов труб в пакете;
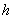 - шаг рядов пакета (расстояние между двумя смежными рядами), см;
- шаг рядов пакета (расстояние между двумя смежными рядами), см;
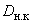 - наружный диаметр коллектора.
- наружный диаметр коллектора.
Сила 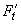 направлена по касательной к наружной поверхности коллектора в сторону направления момента
направлена по касательной к наружной поверхности коллектора в сторону направления момента 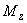 .
.
Единицы измерения сил - кгс, моментов - кгс·см.
7.4. По определенным согласно п.7.3 силам производится расчет напряжений в трубах обоих крайних рядов пакета. При этом применяются формулы, указанные в п.5.3 настоящего РТМ.
Значение коэффициента 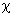 должно приниматься по условиям для труб пакета коллектора (предполагается, что нагрузки, воздействующие на коллектор со стороны станционного трубопровода, определены без учета релаксации).
должно приниматься по условиям для труб пакета коллектора (предполагается, что нагрузки, воздействующие на коллектор со стороны станционного трубопровода, определены без учета релаксации).
8. КРИТЕРИИ ПРОЧНОСТИ
8.1. Оценка прочности трубопроводов должна производиться с учетом действия весовой нагрузки. В первом приближении продольное изгибное напряжение (кгс/см ) от весовой нагрузки можно определять по формуле
) от весовой нагрузки можно определять по формуле
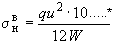 , (30)
, (30)
________________
* Брак оригинала. - Примечание изготовителя базы данных.
где 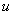 - наибольший пролет между опорами в трубопроводе, м;
- наибольший пролет между опорами в трубопроводе, м;
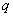 - интенсивность весовой нагрузки, кгс/см.
- интенсивность весовой нагрузки, кгс/см.
8.2. Напряжения от действия внутреннего давления и весовой нагрузки должны удовлетворять условию
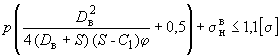 . (31)
. (31)
Допускаемое напряжение 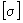 принимается по ОСТ 108.031.02-75.
принимается по ОСТ 108.031.02-75.
8.3. Для высокотемпературного трубопровода напряжения от самокомпенсации, весовой нагрузки и давления должны удовлетворять условиям:
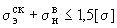 (32)
(32)
для прямолинейных труб и колен при вычислении напряжений по формуле (8) и формуле (24);
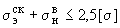 (33)
(33)
для колена при подсчете напряжений по формулам (9) и (25).
8.4. Для низкотемпературного трубопровода напряжения от самокомпенсации и давления должны удовлетворять условию
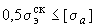 ,
,
где значение 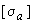 принимается по черт.1 приложения 1 ОСТ 108.031.02-75 в зависимости от числа циклов нагружения трубопровода (т.е. числа включений его в работу или числа отключений его).
принимается по черт.1 приложения 1 ОСТ 108.031.02-75 в зависимости от числа циклов нагружения трубопровода (т.е. числа включений его в работу или числа отключений его).
Для трубопроводов с расчетной температурой 150-250 °С число циклов нагружения рекомендуется принимать с запасом (с превышением над ожидаемым действительным значением) не менее 50%, а при более высокой температуре - с запасом не менее 100%.
Если расчетное число циклов нагружения трубопровода меньше 3000, то принимается значение 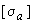 при 3000 циклах.
при 3000 циклах.
8.5. При оценке прочности по п.7.4 предполагается отсутствие глубоких коррозионных повреждений стенки трубопровода (трещины межкристаллитной коррозии, язвенные, повреждения при стояночной коррозии и т.п.). При необходимости учета таких повреждений следует вводить дополнительный запас (ориентировочно не менее четырехкратного по напряжению).
ПРИЛОЖЕНИЕ 1
Рекомендуемое
РАСЧЕТ НЕРАЗВЕТВЛЕННОГО ПЛОСКОГО ТРУБОПРОВОДА,
ИМЕЮЩЕГО ОГРАНИЧИТЕЛИ ПЕРЕМЕЩЕНИЙ
1. В данном приложении на примере трубопровода, показанного на черт.1, указывается методика раскрытия статической неопределимости плоского трубопровода, имеющего ограничители перемещений.
Плоский трубопровод с ограничителями перемещений
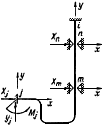
Черт.1
В точках  и
и 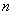 трубопровода (черт.1) установлены ограничители (упоры), не допускающие смещений трубопровода по оси
трубопровода (черт.1) установлены ограничители (упоры), не допускающие смещений трубопровода по оси  .
.
2. Со стороны ограничителей перемещений  и
и 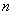 к трубопроводу приложены реактивные силы
к трубопроводу приложены реактивные силы 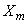 и
и 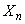 (трение в упорах не учитывается). В концевой заделке
(трение в упорах не учитывается). В концевой заделке  возникают реакции
возникают реакции 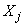 ,
, 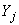 ,
, 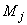 . Перечисленные силовые факторы являются лишними неизвестными.
. Перечисленные силовые факторы являются лишними неизвестными.
3. Поступательные перемещения сечений 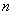 и
и  трубопровода по оси
трубопровода по оси  , конца
, конца  по осям
по осям  ,
,  и угол поворота конца
и угол поворота конца  от действия реактивных силовых факторов определяются следующими формулами (получаются при использовании зависимостей раздела 3 настоящего РТМ).
от действия реактивных силовых факторов определяются следующими формулами (получаются при использовании зависимостей раздела 3 настоящего РТМ).
Перемещения от действия силы 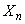 :
:
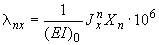 ;
;
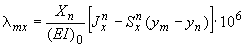 ;
;
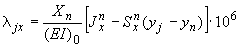 ;
;
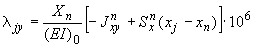 ;
;
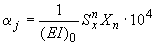 .
.
Перемещения от действия силы 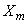 :
:
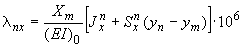 ;
;
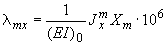 ;
;
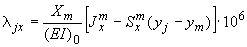 ;
;
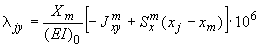 ;
;
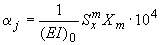 .
.
Перемещения от действия силы 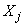 :
:
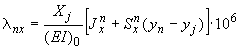 ;
;
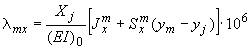 ;
;
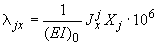 ;
;
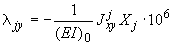 ;
;
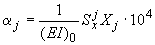 .
.
Перемещения от действия силы 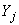 :
:
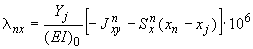 ;
;
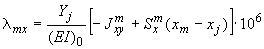 ;
;
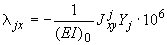 ;
;
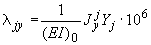 ;
;
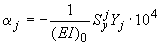 .
.
Перемещения от действия момента 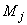 :
:
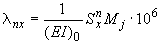 ;
;
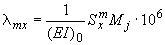 ;
;
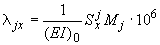 ;
;
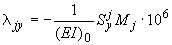 ;
;
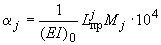 .
.
В приведенных формулах 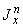 ,
, 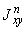 ,
, 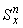 - моменты инерции и статический момент части
- моменты инерции и статический момент части 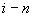 трубопровода относительно координатной системы
трубопровода относительно координатной системы 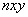 (с началом в точке
(с началом в точке 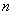 );
); 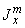 ,
, 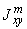 ,
, 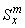 - то же для части
- то же для части 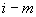 относительно системы
относительно системы 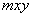 ;
; 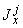 ,
, 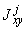 ,
, 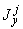 ,
, 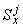 ,
, 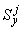 - то же для трубопровода в целом относительно координатной системы
- то же для трубопровода в целом относительно координатной системы 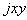 ;
; 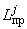 - приведенная длина трубопровода.
- приведенная длина трубопровода.
4. Перемещения вследствие температурного расширения трубопровода и смещение конца  определяются формулами:
определяются формулами:
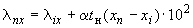 ;
;
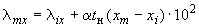 ;
;
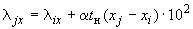 ;
;
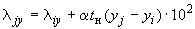 ;
;
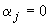 .
.
5. Суммы указанных в пп.3 и 4 выражений для перемещений по оси  сечений
сечений 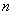 и
и  приравняем нулю, суммы выражений для перемещений сечения
приравняем нулю, суммы выражений для перемещений сечения  - заданным перемещениям
- заданным перемещениям 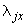 ,
, 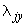 , а сумму выражений для поворота конца
, а сумму выражений для поворота конца  - нулю. Тогда получим следующую систему уравнений:
- нулю. Тогда получим следующую систему уравнений:
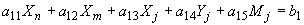 ;
;
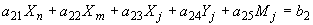 ;
;
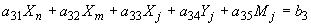 ;
;
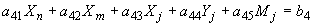 ;
;
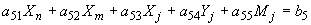 ,
,
где
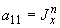 ;
; 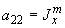 ;
;
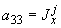 ;
; 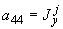 ;
; 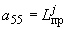 ;
;
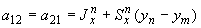 ;
;
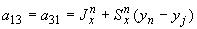 ;
;
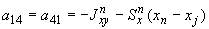 ;
;
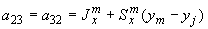 ;
;
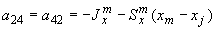 ;
;
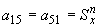 ,
, 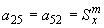 ;
;
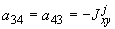 ,
, 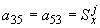 ;
;
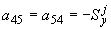 ;
;
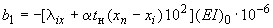 ;
;
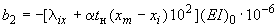 ;
;
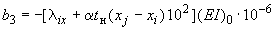 ;
;
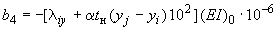 ;
;
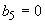 .
.
Решением приведенной системы уравнений определяются все лишние неизвестные.
Моменты инерции и статические моменты для частей трубопровода рекомендуется вычислять в табличной форме (аналогично вычислениям в табл.2 РТМ).
6. Методика построения эпюры изгибающих моментов в трубопроводе, имеющем ограничители перемещений, поясняется черт.2. Здесь равнодействующая реактивных сил перенесена без изменения направления вправо на расстояние 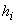 .
.
Построение эпюры моментов
Черт.2
ПРИЛОЖЕНИЕ 2
Рекомендуемое
РАСЧЕТ ПЛОСКОГО РАЗВЕТВЛЕННОГО ТРУБОПРОВОДА
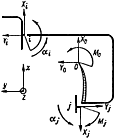
1. Разветвленный трубопровод (трубопроводная система) состоит из промежуточных и концевых участков (черт.1). Концевым участком называется часть трубопровода, заключенная между узлом и концевой защемляющей опорой, а промежуточным участком - часть трубопровода, заключенная между двумя смежными узлами. Так, участок 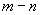 трубопроводной системы, показанной на черт.1, является концевым, а участок
трубопроводной системы, показанной на черт.1, является концевым, а участок 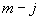 - промежуточным.
- промежуточным.
Плоская трубопроводная система
Черт.1
2. Силы воздействия некоторого промежуточного участка на узлы  и
и  , к которым он присоединен, выражаются следующими формулами (черт.2). (Буквой
, к которым он присоединен, выражаются следующими формулами (черт.2). (Буквой  обозначен тот конец участка, к которому мысленно присоединяется жесткий стержень при расчете по способу упругого центра массы).
обозначен тот конец участка, к которому мысленно присоединяется жесткий стержень при расчете по способу упругого центра массы).
Силовое воздействие промежуточного участка
на узлы трубопроводной системы
Черт.2
Силы воздействия на узел  :
:
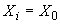 ,
, 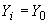 , (1)
, (1)
где
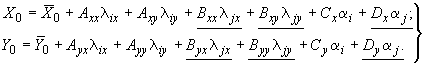 (2)
(2)
Входящие в эти выражения коэффициенты определяются по следующим формулам:
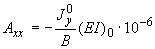 ;
;
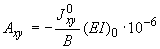 ;
;
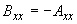 ;
; 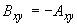 ;
;
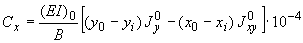 ;
;
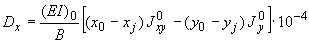 ;
;
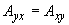 ;
; 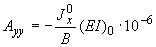 ;
;
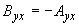 ;
; 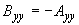 ;
;
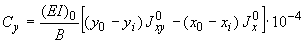 ;
;
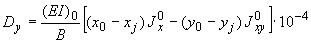 .
.
Величины 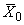 ,
, 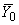 определяются по формулам:
определяются по формулам:
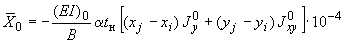 ;
;
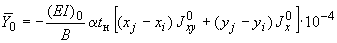
и являются реакциями при условии неподвижности концов  и
и  .
.
Здесь
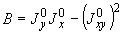 .
.
3. Моменты 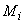 и
и 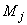 , передающиеся от промежуточного участка на узлы
, передающиеся от промежуточного участка на узлы  и
и  , определяются формулами:
, определяются формулами:
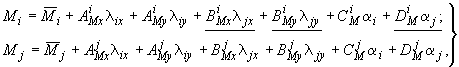 (3)
(3)
где
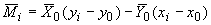 ;
;
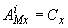 ,
, 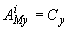 ;
;
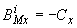 ;
; 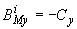 ;
;
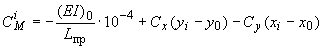 ;
;
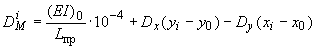 ;
;
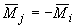 ;
;
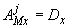 ;
; 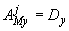 ;
;
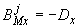 ;
; 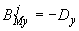 ;
;
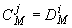 ;
;
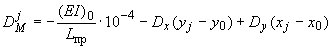 .
.
4. Все приведенные в пп.2 и 3 величины относятся к данному промежуточному участку трубопровода. Определение величин 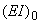 ,
, 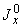 ,
, 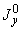 ,
, 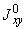 ,
, 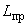 ,
, 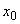 ,
, 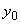 см. в разделе 4 РТМ.
см. в разделе 4 РТМ.
5. Для концевого участка силы и момент, воздействующие на узел, выражаются приведенными формулами для 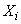 ,
, 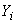 ,
, 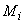 , но подчеркнутые члены следует считать известными (они относятся так же, как и
, но подчеркнутые члены следует считать известными (они относятся так же, как и 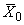 ,
, 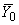 , к заранее определяемым величинам).
, к заранее определяемым величинам).
6. С использованием формул (1) и (3) для сил и моментов записываются для каждого узла уравнения равновесия приложенных к нему силовых факторов
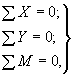 (4)
(4)
где суммирование распространяется на все сходящиеся в данном узле участки.
Решением полученной таким образом системы уравнений определяются поступательные перемещения 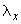 ,
, 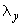 и повороты
и повороты  всех узлов.
всех узлов.
7. По формулам (2) и по формуле
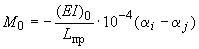
вычисляются реакции (силы в кгс, момент в кгс·м), приложенные в упругом центре масс участка (для концевого участка 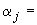 0).
0).
8. Для участков трубопровода строится эпюра изгибающих моментов с целью нахождения наиболее напряженных сечений в прямых трубах и коленах. Способ построения эпюры моментов понятен из черт.3. Если момент 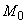 положителен (
положителен (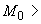 0), то равнодействующая реакций
0), то равнодействующая реакций 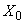 и
и 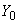 смещается вправо (как на черт.3), если же
смещается вправо (как на черт.3), если же 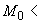 0, то влево.
0, то влево.
Построение эпюры моментов для участка трубопровода
Черт.3
9. С целью упрощения вычислительных операций рекомендуется:
-
на этапе формирования разрешающей системы уравнений (4) принять
 1 (это не отражается на решении системы уравнений);
1 (это не отражается на решении системы уравнений); -
для каждого участка трубопровода принимать свою общую систему координат и производить подсчет геометрических характеристик в этой системе; при этом направления одноименных осей систем координат всех участков должны быть одинаковы.
ПРИЛОЖЕНИЕ 3
Рекомендуемое
РАСЧЕТ ПРОСТРАНСТВЕННОГО РАЗВЕТВЛЕННОГО ТРУБОПРОВОДА
1. В настоящем приложении излагается методика раскрытия статической неопределимости пространственной трубопроводной системы с одним узлом (чертеж). Методика аналогична приведенной в приложении 2 методике для плоского трубопровода. За основные неизвестные принимаются три поступательные и три угловые перемещения узла (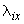 ,
,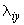 ,
,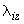 ,
, 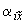 ,
, 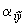 ,
, 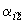 ).
).
Пространственный разветвленный трубопровод
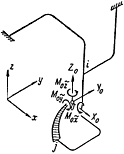
2. Силы воздействия некоторого участка 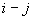 трубопровода на узел
трубопровода на узел  выражаются формулами:
выражаются формулами:
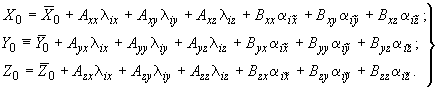 (1)
(1)
3. Величины 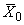 ,
, 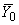 и коэффициенты при неизвестных в первых двух формулах (1) определяются следующими формулами:
и коэффициенты при неизвестных в первых двух формулах (1) определяются следующими формулами:
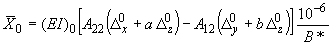 ;
;
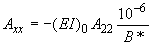 ;
;
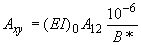 ;
;
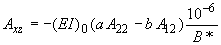 ;
;
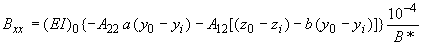 ;
;
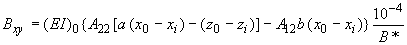 ;
;
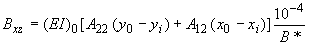 ;
;
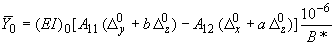 ;
;
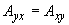 ;
;
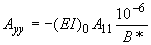 ;
;
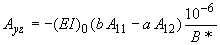 ;
;
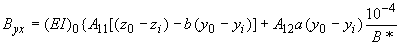 ;
;
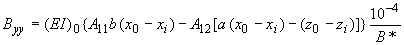 ;
;
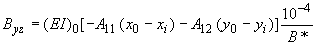 ,
,
где
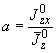 ;
; 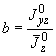 ;
;
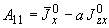 ;
;
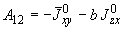 ;
;
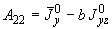 ;
;
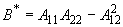 ;
;
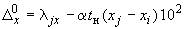 ;
;
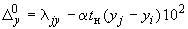 ;
;
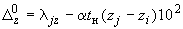 .
.
4. Величина 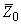 и коэффициенты в третьей формуле (1) определяются следующими зависимостями:
и коэффициенты в третьей формуле (1) определяются следующими зависимостями:
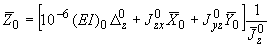 ;
;
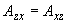 ;
; 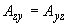 ;
;
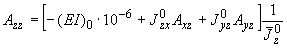 ;
;
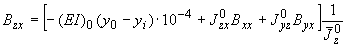 ;
;
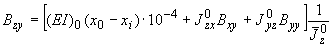 ;
;
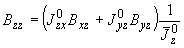 .
.
5. Моменты, действующие на узел со стороны участка, выражаются формулами:
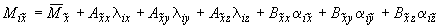 ;
;
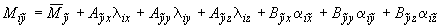 ;
;
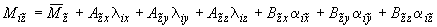 ,
,
где
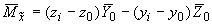 ;
;
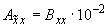 ;
;
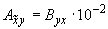 ;
;
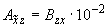 ;
;
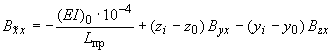 ;
;
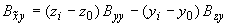 ;
;
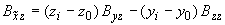 ;
;
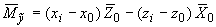 ;
;
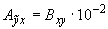 ;
; 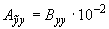 ;
;
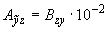 ;
; 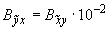 ;
;
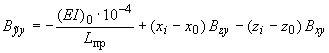 ;
;
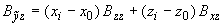 ;
;
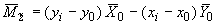 ;
;
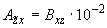 ;
; 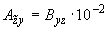 ;
;
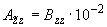 ;
;
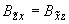 ;
; 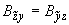 ;
;
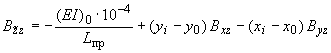 .
.
6. Все приведенные в пп.3-5 величины относятся к данному участку трубопровода. Определение величин 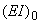 ,
, 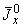 ,
, 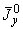 ,
, 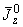 ,
, 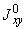 ,
, 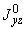 ,
, 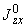 ,
, 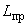 ,
, 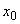 ,
, 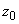 ,
, 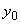 см. в разделе 6 настоящего РТМ.
см. в разделе 6 настоящего РТМ.
7. Условия равновесия сил и моментов, приложенных к узлу, выражаются системой уравнений:
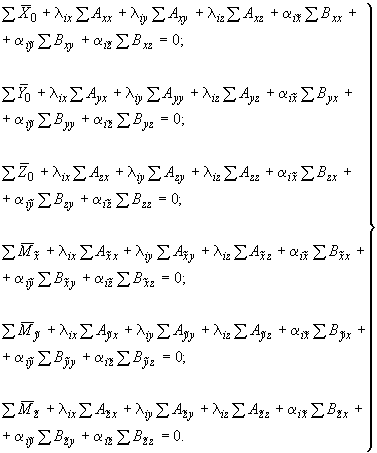 (2)
(2)
Суммирование распространяется на все участки трубопровода.
Решением этой системы уравнений определяются перемещения 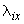 ,
, 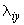 ,
, 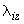 (в см) и углы поворота
(в см) и углы поворота 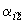 ,
, 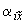 ,
, 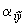 (в радианах) узла. Следует учитывать, что матрица коэффициентов системы уравнений симметричная.
(в радианах) узла. Следует учитывать, что матрица коэффициентов системы уравнений симметричная.
8. После решения системы уравнений (2) для каждого участка вычисляются по формулам (1) силы 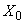 ,
, 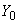 ,
, 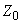 (в кгс), а по формулам:
(в кгс), а по формулам:
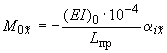 ;
;
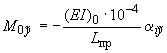 ;
;
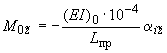
- моменты (в кгс·м), приложенные в упругом центре масс участка (к концу воображаемого жесткого стержня, см. чертеж).
9. Так же, как в плоском трубопроводе (см. приложение 2), строятся эпюры моментов на чертежах проекций каждого трубопроводного участка. Для выявленных с помощью этих эпюр наиболее нагруженных сечений прямолинейных труб и колен вычисляются напряжения и производится оценка прочности.
10. Указанные в п.9 рекомендуемого приложения 2 рекомендации, служащие для упрощения расчета, распространяются и на пространственный разветвленный трубопровод.
ПРИЛОЖЕНИЕ 4
Рекомендуемое
ПРИМЕРЫ РАСЧЕТА
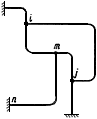
Пример 1.
Произвести ориентировочную оценку компенсирующей способности плоского неразветвленного трубопровода, показанного на черт.1. Трубопровод транспортирует конденсат с расчетными параметрами 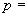 154 кгс/см
154 кгс/см ,
, 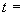 343 °С и выполнен из труб сечением
343 °С и выполнен из труб сечением 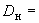 133 мм,
133 мм, 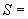 10 мм. Колено около барабана и прилегающие к нему прямолинейные участки длиной по 200 мм имеют толщину
10 мм. Колено около барабана и прилегающие к нему прямолинейные участки длиной по 200 мм имеют толщину 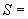 12 мм. Овальность всех колен 10%. Материал труб - сталь марки 20. Модуль упругости и коэффициент линейного расширения материала, соответствующие расчетной температуре:
12 мм. Овальность всех колен 10%. Материал труб - сталь марки 20. Модуль упругости и коэффициент линейного расширения материала, соответствующие расчетной температуре: 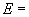 1,86·10
1,86·10 кгс/см
кгс/см и
и 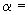 13,35·10
13,35·10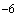 1/°С, ожидаемое число пусков 7000. Направления смещений конца трубопровода, подсоединенного к барабану, показаны на черт.1 стрелками, а величины смещений (в см) - числами около стрелок. Другой конец трубопровода неподвижен. Согласно п.1.8 РТМ трубопровод является низкотемпературным.
1/°С, ожидаемое число пусков 7000. Направления смещений конца трубопровода, подсоединенного к барабану, показаны на черт.1 стрелками, а величины смещений (в см) - числами около стрелок. Другой конец трубопровода неподвижен. Согласно п.1.8 РТМ трубопровод является низкотемпературным.
Трубопровод, рассматриваемый в примерах 1 и 2
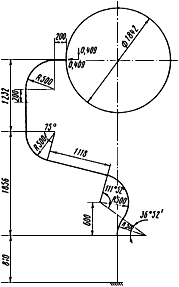
Черт.1
Полагая, что температура окружающего воздуха 10 °С, находим температуру нагрева  343-10=333 °С.
343-10=333 °С.
Определяем безразмерные коэффициенты для колена, необходимые для определения коэффициента податливости и коэффициента интенсификации напряжений, причем толщину стенки для всех колен принимаем постоянной  10 мм.
10 мм.
Согласно п.2.5 РТМ
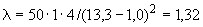 ;
;
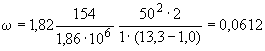 .
.
Определяем  1,4 (см. табл.1 РТМ). По черт.7 РТМ находим
1,4 (см. табл.1 РТМ). По черт.7 РТМ находим  1,15. Согласно п.2.9 вычисляем момент инерции поперечного сечения трубы:
1,15. Согласно п.2.9 вычисляем момент инерции поперечного сечения трубы:
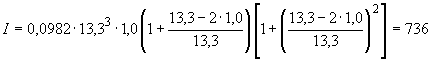 см
см .
.
Момент сопротивления 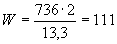 см
см .
.
По формулам (3) РТМ определяем компенсируемые перемещения по осям:
-
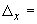 0-(0,409)-13,35·10
0-(0,409)-13,35·10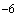 ·333(1,621-0,70)·10
·333(1,621-0,70)·10 =0;
=0;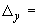 0-(-0,409)-13,35·10
0-(-0,409)-13,35·10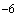 ·333(0-3,898)·10
·333(0-3,898)·10 =1,32 см.
=1,32 см.
Компенсируемое перемещение 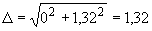 см.
см.
Расстояние между концами трубопровода  4 м, его длина
4 м, его длина  5,66 м, часть длины трубопровода, приходящаяся на все его колена,
5,66 м, часть длины трубопровода, приходящаяся на все его колена,  2,74 м.
2,74 м.
Следовательно (по п.6.1.2 РТМ)
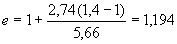 .
.
По черт.20 РМТ при 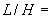 1,45 находим
1,45 находим 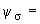 15. В соответствии с п.4.5.2 принимаем
15. В соответствии с п.4.5.2 принимаем 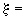 1,21. По ОСТ 108.031.02-75 поправки на толщину стенки составят для прямой трубы
1,21. По ОСТ 108.031.02-75 поправки на толщину стенки составят для прямой трубы 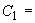 0,05 см, для колена
0,05 см, для колена 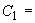 0,06 см, а коэффициенты прочности
0,06 см, а коэффициенты прочности 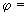 1 и
1 и 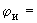 0,8.
0,8.
Теперь можно переходить к определению эквивалентных напряжений.
Для прямой трубы согласно п.6.1.5 РТМ
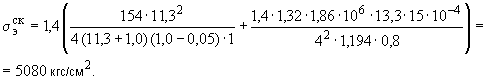
Для колена по п.6.1.5 РТМ
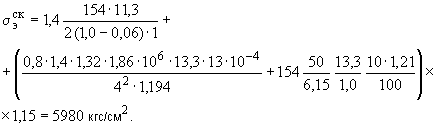
Согласно п.8.4 РТМ расчетное число циклов равно 7000+7000=14000. Допустимая амплитуда напряжений по ОСТ 108.031.02-75 будет 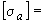 2000 кгс/см
2000 кгс/см .
.
Условие прочности по п.8.4 РТМ не выполняется:
-
0,5·6980>2600 кгс/см
 .
.
Учитывая, что расчетные напряжения не намного превышают допустимые напряжения, целесообразно проведение расчета по уточненной методике.
Определим равнодействующую 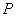 реактивных сил, возникающих в концевой заделке трубопровода. По черт.19 получаем
реактивных сил, возникающих в концевой заделке трубопровода. По черт.19 получаем 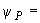 200. Жесткость трубопровода, определяемая по п.6.1.2 РТМ, будет
200. Жесткость трубопровода, определяемая по п.6.1.2 РТМ, будет
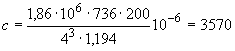 кгс/см.
кгс/см.
Реакция опоры 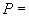 3570·1,32=4700 кгс.
3570·1,32=4700 кгс.
Пример 2. Произвести уточненный расчет на самокомпенсацию плоского неразветвленного трубопровода, рассмотренного в примере 1.
За эталонную жесткость при определении приведенных длин отрезков принимается жесткость труб с толщиной стенки 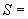 10 мм. Характеристики отрезков из этих труб определены в примере 1. Для труб с
10 мм. Характеристики отрезков из этих труб определены в примере 1. Для труб с 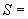 12 мм аналогично получаем
12 мм аналогично получаем 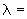 1,36;
1,36; 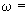 0,0622;
0,0622; 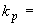 1,4;
1,4; 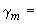 1,1;
1,1; 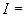 842 см
842 см ;
; 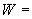 127 см
127 см .
.
Подсчет геометрических характеристик трубопровода выполнен в табл.1, а собственных моментов инерции отрезков - в табл.2. Разбивка на отрезки показана на черт.2.
Таблица 1
Расчет геометрических характеристик плоского трубопровода
|
Номер отрезка ( |
Приведенная длина |
Координаты центров масс, м |
Статические моменты, м |
Моменты инерции, м |
||||
|
|
|
|
|
|
|
|
||
|
1 |
0,23 |
3,9 |
0,60 |
0,9 |
0,14 |
3,51 |
0,08 |
0,54 |
|
2 |
1,26 |
3,75 |
0,15 |
4,73 |
0,19 |
17,35 |
0,03 |
0,71 |
|
3 |
0,23 |
3,30 |
0 |
0,76 |
0 |
2,51 |
0 |
0 |
|
4 |
0,61 |
2,93 |
0 |
1,78 |
0 |
5,11 |
0 |
0 |
|
5 |
0,92 |
2,37 |
0,09 |
2,18 |
0,08 |
5,16 |
0,01 |
0,20 |
|
6 |
1,12 |
3,03 |
0,91 |
3,39 |
1,02 |
10,3 |
0,93 |
3,08 |
|
7 |
0,68 |
1,76 |
1,66 |
1,20 |
1,13 |
2,11 |
1,88 |
1,99 |
|
8 |
0,68 |
1,34 |
1,82 |
0,91 |
1,24 |
1,22 |
2,26 |
1,66 |
|
9 |
0,44 |
0,97 |
1,65 |
0,43 |
0,73 |
0,42 |
1,20 |
0,71 |
|
10 |
0,81 |
0,41 |
1,62 |
0,33 |
1,31 |
0,14 |
2,12 |
0,53 |
|
|
|
|
|
|
|
|
|
|
|
Примечание. |
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
||||||
Таблица 2
Вычисление собственных моментов инерции отрезков трубопровода
|
Номер отрезка |
|
|
|
|
|
|
|
|
|
± |
||||
|
1 |
0,23 |
0,20 |
0 |
0,009 |
0 |
0 |
|
2 |
1,26 |
0,50 |
0,50 |
0,315 |
0,314 |
0,314 |
|
3 |
0,23 |
0 |
0,20 |
0 |
0,092 |
0 |
|
4 |
0,61 |
0 |
0,53 |
0 |
0,165 |
0 |
|
5 |
0,92 |
0,37 |
0,48 |
0,126 |
0,212 |
0,163 |
|
6 |
1,12 |
1,08 |
0,29 |
1,310 |
0,094 |
0,350 |
|
7 |
0,68 |
0,36 |
0,30 |
0,088 |
0,061 |
0,073 |
|
8 |
0,68 |
0,08 |
0,47 |
0,004 |
0,150 |
0,026 |
|
9 |
0,44 |
0,10 |
0,30 |
0,004 |
0,040 |
0,013 |
|
10 |
0,81 |
0 |
0,81 |
0 |
0,532 |
0 |
|
|
1,856 |
1,660 |
0,939 |
|||
|
|
0,155 |
0,138 |
0,078 |
Разбивка на отрезки и эпюра изгибающих моментов трубопровода, рассматриваемого в примере 2
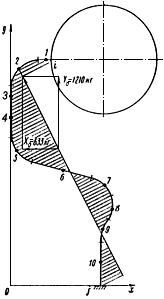
Черт.2
По формулам (4) РТМ определяем реактивные силы опоры:
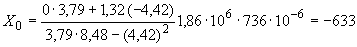 кгс,
кгс,
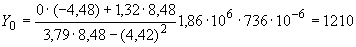 кгс.
кгс.
Эпюра изгибающих моментов представлена на черт.2. Видно, что наиболее нагруженным является колено 5. Действующий в нем изгибающий момент 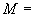 930 кгс·м увеличивает кривизну колена и, следовательно, по п.4.3.2 РТМ является положительным. Осевая сила в колене
930 кгс·м увеличивает кривизну колена и, следовательно, по п.4.3.2 РТМ является положительным. Осевая сила в колене 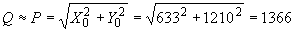 кгс.
кгс.
Определим эквивалентное напряжение.
Согласно п.4.5.1 РТМ, принимая 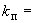 1,4, находим при площади поперечного сечения
1,4, находим при площади поперечного сечения 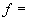 38,7 см
38,7 см
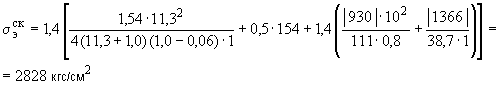
По п.4.5.2 РТМ при 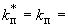 1,4
1,4
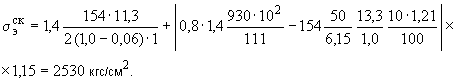
При 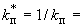 1/1,4=0,714
1/1,4=0,714 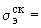 3050 кгс/см
3050 кгс/см . Это значение должно приниматься при оценке прочности. Проверка выполнения условия прочности производится так же, как в примере 1. Имеем 0,5·3050<2600 кгс/см
. Это значение должно приниматься при оценке прочности. Проверка выполнения условия прочности производится так же, как в примере 1. Имеем 0,5·3050<2600 кгс/см . Условие прочности удовлетворяется.
. Условие прочности удовлетворяется.
Для окончательной оценки прочности трубопровода необходима проверка также по условию (31) РТМ.
Табл.3 иллюстрирует влияние упрощений при определении геометрических характеристик трубопровода на расчетные значения 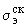 и реактивной силы.
и реактивной силы.
Таблица 3
Результаты расчета трубопровода при разных вариантах определения геометрических характеристик трубопровода
|
Вариант расчета геометрических характеристик трубопровода |
Реакция опоры, кгс |
Максимальное эквивалентное напряжение, кгс/см |
|
С учетом собственных моментов инерции всех отрезков (по п 4.7 РТМ) |
1366 |
2720 |
|
То же, но без учета собственных моментов инерции (по п.4.7.16) |
1690 |
3190 |
|
То же, но без учета собственных моментов инерции и при исключении отрезков 7 и 8 (по п.4.7.15) |
2440 |
3580 |
Пример 3.
Произвести ориентировочную оценку прочности плоского неразветвленного трубопровода, показанного на черт.3. Трубопровод транспортирует пар с расчетными параметрами 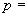 149 кгс/см
149 кгс/см ,
, 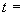 500 °С и выполнен из труб сечением
500 °С и выполнен из труб сечением 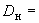 27,3 см,
27,3 см, 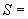 2,0 см. Наибольшее расстояние между опорами
2,0 см. Наибольшее расстояние между опорами 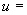 7,5 м. Колена имеют радиус
7,5 м. Колена имеют радиус 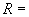 130 см, возможная овальность сечения не более 8%. Материал труб - сталь марки 12Х1МФ. Модуль упругости, коэффициент линейного расширения и допускаемое напряжение, соответствующие расчетной температуре:
130 см, возможная овальность сечения не более 8%. Материал труб - сталь марки 12Х1МФ. Модуль упругости, коэффициент линейного расширения и допускаемое напряжение, соответствующие расчетной температуре: 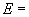 1,82·10
1,82·10 кгс/см
кгс/см ,
, 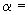 13,2·10
13,2·10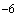 1/°С,
1/°С, 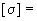 1130 кгс/см
1130 кгс/см . Направления смещений защемленных концов указаны на черт.3 стрелками, а их величины (в см) - числами около стрелок. Интенсивность весовой нагрузки
. Направления смещений защемленных концов указаны на черт.3 стрелками, а их величины (в см) - числами около стрелок. Интенсивность весовой нагрузки 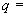 2,4 кгс/см. Согласно п.1.8 РТМ трубопровод является высокотемпературным.
2,4 кгс/см. Согласно п.1.8 РТМ трубопровод является высокотемпературным.
Трубопровод, рассматриваемый в примерах 3 и 4
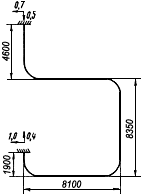
Черт.3
Полагая, что температура окружающего воздуха 10 °С, находим температуру нагрева 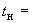 500-10=490 °С.
500-10=490 °С.
Определяем безразмерные коэффициенты для колена, необходимые для определения коэффициента податливости и коэффициента интенсификации напряжений.
Согласно п.2.5 РТМ
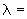 130·2,0·4/(27,3-2,0)
130·2,0·4/(27,3-2,0) =1,625;
=1,625;
 1,82·149·130
1,82·149·130 ·2/1,82·10
·2/1,82·10 ·20(27,3-2,0)=0,0995.
·20(27,3-2,0)=0,0995.
Определяем  1,3 (см. черт.5 и табл.1 РТМ).
1,3 (см. черт.5 и табл.1 РТМ).
Вычисляем момент инерции поперечного сечения трубы (п.2.9):
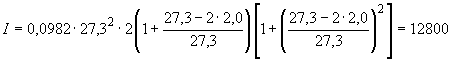 см
см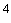 .
.
Момент сопротивления 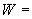 939 см
939 см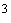 . Площадь поперечного сечения
. Площадь поперечного сечения 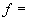 159 см
159 см .
.
По формулам (3) РТМ определяем компенсируемые перемещения по осям:
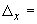 -0,7+1,0-13,2·10
-0,7+1,0-13,2·10 ·490[-4,0-(-4,0)]·10
·490[-4,0-(-4,0)]·10 =0,3 см,
=0,3 см,
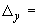 -0,5-0,4-13,2·10
-0,5-0,4-13,2·10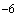 ·490[8,65-(-2,0)]·10
·490[8,65-(-2,0)]·10 =-7,79 см.
=-7,79 см.
Компенсируемое перемещение 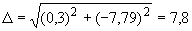 см.
см.
Расстояние между концами трубопровода 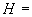 11,05 м, его длина
11,05 м, его длина 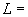 28,81 м; часть длины трубопровода, приходящаяся на все его колена
28,81 м; часть длины трубопровода, приходящаяся на все его колена 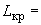 8,16 м.
8,16 м.
Следовательно (по п.6.1.2 РТМ)
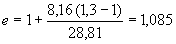 .
.
По черт.20 РТМ для 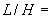 2,61 получаем
2,61 получаем 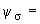 2,6.
2,6.
Согласно ОСТ 108.031.02-75 для прямолинейных труб 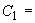 0,095 мм, для колен
0,095 мм, для колен 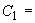 0,113 мм,
0,113 мм, 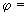 1,
1, 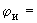 0,8. В соответствии с черт.3 РТМ
0,8. В соответствии с черт.3 РТМ 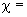 0,58.
0,58.
Толщина стенки рассматриваемого трубопровода удовлетворяет требованиям ОСТ 108.031.02-75. Поэтому овальность при определении напряжений не учитываем. Поскольку 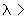 1 и
1 и 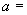 0, для определения напряжений используем только формулу (24) РТМ:
0, для определения напряжений используем только формулу (24) РТМ:
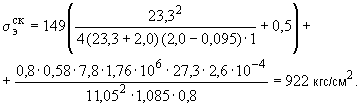
Напряжение от весовой нагрузки по формуле (30) РТМ
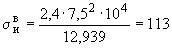 кгс/см
кгс/см .
.
Условие прочности (31) РТМ удовлетворяется:
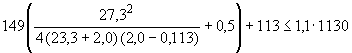 .
.
Условие прочности (32) РТМ также удовлетворяется:
-
922+113<1,5·1130.
Определим реактивное усилие концевой заделки. По черт.19 РТМ имеем 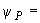 15,8. Жесткость трубопровода
15,8. Жесткость трубопровода
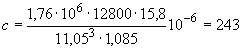 кгс/см
кгс/см .
.
Реакция опоры  243·7,8=1900 кгс.
243·7,8=1900 кгс.
Пример 4. Произвести расчет на самокомпенсацию плоского неразветвленного трубопровода, рассмотренного в примере 3.
Разбивка трубопровода на отрезки и принятая система координат показаны на черт.4.
Разбивка на отрезки и эпюра изгибающих моментов трубопровода, рассматриваемого в примере 4
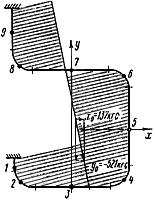
Черт.4
Подсчет геометрических характеристик трубопровода выполнен в табл.4, а собственных моментов инерции отрезков - в табл.5.
Таблица 4
Расчет геометрических характеристик плоского трубопровода
|
Номер отрезка ( |
Приведенная длина |
Координаты центров масс, м |
Статические моменты, м |
Моменты инерции, м |
||||
|
|
|
|
|
|
|
|
||
|
1 |
0,60 |
-2,3 |
-4,0 |
-1,4 |
-2,4 |
3,2 |
9,6 |
5,6 |
|
2 |
2,65 |
-3,8 |
-3,6 |
-10,1 |
-9,5 |
37,3 |
34,2 |
36,4 |
|
3 |
5,50 |
-4,2 |
0 |
-23,1 |
0 |
97,5 |
0 |
0 |
|
4 |
2,65 |
-3,8 |
3,6 |
-10,1 |
9,5 |
37,4 |
34,2 |
-36,4 |
|
5 |
5,75 |
0 |
4,0 |
0 |
23,0 |
0,0 |
92,0 |
0 |
|
6 |
2,65 |
3,8 |
3,6 |
10,1 |
9,5 |
37,4 |
34,2 |
36,4 |
|
7 |
5,50 |
4,2 |
0 |
23,1 |
0 |
97,5 |
0 |
0 |
|
8 |
2,65 |
4,6 |
-3,6 |
12,2 |
-9,5 |
56,2 |
34,2 |
-43,8 |
|
9 |
3,30 |
7,0 |
-4,0 |
23,1 |
- 13,2 |
161,7 |
52,8 |
-92,5 |
|
|
|
|
|
|
|
|
|
|
|
Примечание. |
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
||||||
Таблица 5
Вычисление собственных моментов инерции отрезков трубопровода
|
Номер отрезка |
|
|
|
|
|
|
|
|
|
± |
||||
|
1 |
0,60 |
0 |
0,60 |
0 |
0,216 |
0 |
|
2 |
2,65 |
1,3 |
1,30 |
4,49 |
4,490 |
-4,49 |
|
3 |
5,50 |
5,5 |
0 |
166,00 |
0 |
0 |
|
4 |
2,65 |
1,3 |
1,30 |
4,49 |
4,490 |
4,49 |
|
5 |
5,75 |
0 |
5,75 |
0 |
190,000 |
0 |
|
6 |
2,65 |
1,3 |
1,30 |
4,49 |
4,490 |
-4,49 |
|
7 |
5,50 |
5,5 |
0 |
166,00 |
0 |
0 |
|
8 |
2,65 |
1,3 |
1,30 |
4,49 |
4,490 |
-4,49 |
|
9 |
3,30 |
0 |
3,30 |
0 |
36,000 |
0 |
|
|
350,00 |
244,200 |
-8,98 |
|||
|
|
29,20 |
20,300 |
-0,748 |
По формулам (4) РТМ определяем реактивные силы опоры:
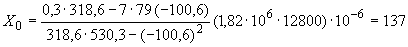 кгс;
кгс;
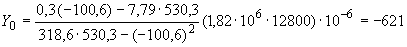 кгс.
кгс.
Компенсируемые перемещения, модуль упругости и момент инерции поперечного сечения см. в примере 3.
Коэффициент релаксации компенсационных напряжений согласно черт.4 РТМ 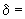 0,8.
0,8.
По п.4.1.4 РТМ находим реактивные силы в рабочем состоянии после релаксации:
-
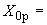 137(1-0,8)=27 кгс;
137(1-0,8)=27 кгс;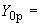 -621(1-0,8)=-124 кгс.
-621(1-0,8)=-124 кгс.
Учитывая значение модуля упругости в холодном состоянии 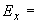 2,12·10
2,12·10 кгс/см
кгс/см , находим силы в холодном состоянии:
, находим силы в холодном состоянии:
-
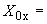 137(-0,8·2,12·10
137(-0,8·2,12·10 /1,82·10
/1,82·10 )=-128 кгс;
)=-128 кгс;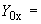 -621(-0,8·2,12·10
-621(-0,8·2,12·10 /1,82·10
/1,82·10 )=578 кгс.
)=578 кгс.
Результирующее усилие до релаксации
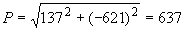 кгс.
кгс.
На черт.4 представлена эпюра изгибающих моментов. Видно, что наибольший момент 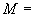 637·4,98=3170 кгс·м действует на криволинейном отрезке 2.
637·4,98=3170 кгс·м действует на криволинейном отрезке 2.
Толщина стенки рассматриваемого трубопровода удовлетворяет требованиям ОСТ 108.031.02-75 с учетом поправки на овальность. Поэтому согласно п.4.4.2 РТМ овальность колен при определении напряжений не учитываем. Поскольку 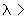 1 и принимается
1 и принимается 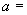 0, для определения напряжений используем только формулу (8) РТМ. Учитывая величину площади поперечного сечения
0, для определения напряжений используем только формулу (8) РТМ. Учитывая величину площади поперечного сечения 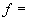 159 см
159 см , имеем (
, имеем (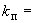 1,4)
1,4)
Условие прочности по формуле (32) РТМ удовлетворяется:
-
772+113<1,5·1130.
Проверка по условию прочности (31) выполнена в примере 3.
Пример 5.
Произвести ориентировочную оценку компенсирующей способности пространственного трубопровода, показанного на черт.5. Трубопровод выполнен из труб сечением  13,3 см,
13,3 см,  1,7 см. Сталь марки 12Х1МФ. Радиус колен
1,7 см. Сталь марки 12Х1МФ. Радиус колен 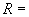 60 см; начальная овальность сечения не более 8%. Расчетные параметры среды
60 см; начальная овальность сечения не более 8%. Расчетные параметры среды 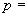 140 кгс/см
140 кгс/см ,
, 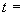 560 °С. Смещения концов трубопровода показаны на черт.3 стрелками, а их величины (в см) - числами около стрелок. Промежуточные опоры отсутствуют. Интенсивность весовой нагрузки с учетом изоляции
560 °С. Смещения концов трубопровода показаны на черт.3 стрелками, а их величины (в см) - числами около стрелок. Промежуточные опоры отсутствуют. Интенсивность весовой нагрузки с учетом изоляции 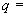 1,15 кгс/см.
1,15 кгс/см.
Трубопровод, рассматриваемый в примерах 5 и 6
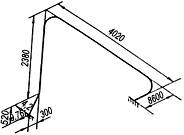
Черт.5
Характеристики материала, соответствующие расчетной температуре: 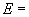 1,74.10
1,74.10 кгс/см
кгс/см ,
, 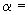 13,5·10
13,5·10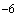 1/°С,
1/°С, 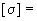 590 кгс/см
590 кгс/см . Температура монтажа 10 °С. Момент инерции поперечного сечения
. Температура монтажа 10 °С. Момент инерции поперечного сечения 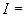 1065 см
1065 см . Момент сопротивления
. Момент сопротивления 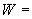 161 см
161 см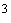 . Трубопровод относится к категории высокотемпературных трубопроводов (см. п.1.8 РТМ).
. Трубопровод относится к категории высокотемпературных трубопроводов (см. п.1.8 РТМ).
Определяем для колена: 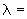 3,0;
3,0; 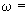 0,054 и по этим значениям находим
0,054 и по этим значениям находим 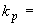 1,00.
1,00.
По формулам (16) РТМ определяем компенсируемые перемещения по осям:
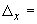 0-0,76-13,5·10
0-0,76-13,5·10 ·550(0,86-0,3)·10
·550(0,86-0,3)·10 =-1,18 см,
=-1,18 см,
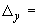 0+4,2-13,5·10
0+4,2-13,5·10 ·550(0,402-0)·10
·550(0,402-0)·10 =1,16 см,
=1,16 см,
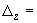 0-0-13,5·10
0-0-13,5·10 ·550(0-(0-2,9))·10
·550(0-(0-2,9))·10 =2,15 см.
=2,15 см.
Компенсируемое перемещение 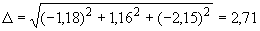 см.
см.
Расстояние между концами трубопровода 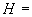 5,0 м; его длина
5,0 м; его длина 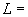 7,3 м;
7,3 м; 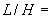 1,46. Поскольку
1,46. Поскольку 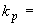 1,00, приведенная длина трубопровода равна его действительной длине.
1,00, приведенная длина трубопровода равна его действительной длине.
По черт.20 РТМ получаем 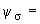 15,0. Согласно ОСТ 108.031.02-75 для прямолинейной трубы
15,0. Согласно ОСТ 108.031.02-75 для прямолинейной трубы 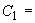 0,81, для колена
0,81, для колена 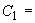 0,96 мм;
0,96 мм; 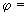 1,
1, 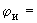 0,6. В соответствии с черт.3 РТМ
0,6. В соответствии с черт.3 РТМ 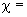 0,45. По п.2.8 РТМ принимаем
0,45. По п.2.8 РТМ принимаем 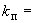 1,4.
1,4.
Толщина стенки рассматриваемого трубопровода удовлетворяет требованиям ОСТ 108.031.02-75. Поэтому овальность при определении напряжений не учитываем. Поскольку 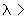 1 и
1 и 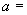 0, для определения напряжений используем только формулу (24) РТМ:
0, для определения напряжений используем только формулу (24) РТМ:
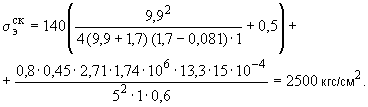
Полагая, что в трубопроводе отсутствуют промежуточные опоры, имеем 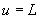 и получим по формуле (30) РТМ, что напряжения от весовой нагрузки
и получим по формуле (30) РТМ, что напряжения от весовой нагрузки
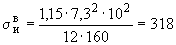 кгс/см
кгс/см .
.
Условие прочности (31) РТМ не удовлетворяется:
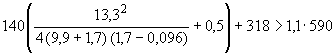 .
.
Условие прочности по соотношению (32) РТМ также не удовлетворяется:
-
2500+318>1,5·590.
Определим реактивное усилие в защемленном конце. По черт.19 РТМ имеем 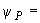 200. Жесткость трубопровода
200. Жесткость трубопровода
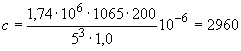 кгс/см.
кгс/см.
Реактивная сила 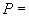 2960·2,71=8000 кгс.
2960·2,71=8000 кгс.
Пример 6. Произвести расчет на самокомпенсацию пространственного неразветвленного трубопровода, рассмотренного в примере 5.
Разбивка трубопровода на отрезки и принятая система координат показаны на черт.6.
Проекции трубопровода с эпюрами моментов
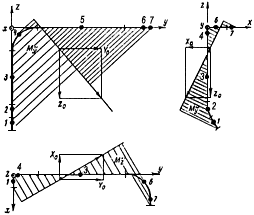
Черт.6
Вычисления геометрических характеристик трубопроводов приведены в табл.6, а собственных моментов инерции отрезков - в табл.7.
Таблица 6
Расчет геометрических характеристик пространственного трубопровода
|
Но- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3)·(6), м |
(4)·(7), м |
(5)·(8), м |
(4)·(6), м |
(5)·(7), м |
(5)·(6), м |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1 |
0,41 |
0,220 |
0 |
-2,730 |
0,09 |
0 |
-1,12 |
0,020 |
0 |
3,06 |
0 |
0 |
-0,246 |
|
2 |
0,31 |
0,030 |
0 |
-2,390 |
0,01 |
0 |
-0,74 |
0 |
0 |
1,77 |
0 |
0 |
-0,024 |
|
3 |
1,62 |
0 |
0 |
-1,420 |
0 |
0 |
-2,30 |
0 |
0 |
3,26 |
0 |
0 |
0 |
|
4 |
0,94 |
0 |
0,175 |
-0,175 |
0 |
0,16 |
-0,16 |
0 |
0,03 |
0,03 |
0 |
-0,03 |
0 |
|
5 |
2,82 |
0 |
2,010 |
0 |
0 |
5,66 |
0 |
0 |
11,4 |
0 |
0 |
0 |
0 |
|
6 |
0,94 |
0,175 |
3,840 |
0 |
0,16 |
3,61 |
0 |
0,028 |
14,0 |
0 |
0,614 |
0 |
0 |
|
7 |
0,26 |
0,730 |
4,020 |
0 |
0,19 |
1,04 |
0 |
0,131 |
4,18 |
0 |
0,763 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание. |
|
0,179 |
14,61 |
5,57 |
0,73 |
6,17 |
-0,27 |
||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
Таблица 7
Вычисление собственных моментов инерции отрезков трубопровода
|
Номер отрезка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
± |
± |
± |
|||||
|
1 |
0,41 |
0,205 |
0 |
0,36 |
0,017 |
0 |
0,053 |
0 |
0 |
-0,0303 |
|
2 |
0,31 |
0,080 |
0 |
0,30 |
0,002 |
0 |
0,028 |
0 |
0 |
-0,0074 |
|
3 |
1,62 |
0 |
0 |
1,62 |
0 |
0 |
4,250 |
0 |
0 |
0 |
|
4 |
0,94 |
0 |
0,60 |
0,60 |
0 |
0,338 |
0,338 |
0 |
0,338 |
0 |
|
5 |
2,82 |
0 |
2,82 |
0 |
0 |
22,800 |
0 |
0 |
0 |
0 |
|
6 |
0,94 |
0,600 |
0,60 |
0 |
0,338 |
0,338 |
0 |
0,338 |
0 |
0 |
|
7 |
0,26 |
0,260 |
0 |
0 |
0,018 |
0 |
0 |
0 |
0 |
0 |
|
|
0,375 |
23,500 |
4,669 |
0,338 |
0,338 |
-0,0377 |
||||
|
|
0,031 |
1,960 |
0,388 |
0,028 |
0,028 |
-0,003 |
Вычисляем моменты инерции:
-
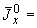 16,57+5,96=22,53 м
16,57+5,96=22,53 м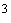 ;
;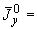 5,96+0,182=6,15 м
5,96+0,182=6,15 м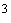 ;
;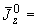 16,57+0,182=16,75 м
16,57+0,182=16,75 м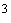 .
.
Формируем систему уравнений (14) РТМ:
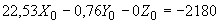 ;
;
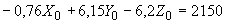 ;
;
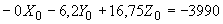 .
.
Решением ее определяем реактивные силы на конце  (или в упругом центре масс):
(или в упругом центре масс):
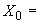 -91,5 кгс;
-91,5 кгс; 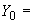 156,6 кгс;
156,6 кгс; 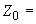 -180,3 кгс.
-180,3 кгс.
Коэффициент релаксации компенсационных напряжений согласно черт.4 РТМ 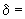 1,0. Следовательно, согласно п.4.1.3 РТМ в рабочем состоянии после релаксации компенсационные усилия исчезнут:
1,0. Следовательно, согласно п.4.1.3 РТМ в рабочем состоянии после релаксации компенсационные усилия исчезнут:
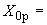 -91,5(1-1)=0;
-91,5(1-1)=0;
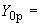 156,6(1-1)=0;
156,6(1-1)=0;
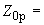 -180,3(1-1)=0.
-180,3(1-1)=0.
Значение модуля упругости в холодном состоянии 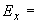 2,12·10
2,12·10 кгс/см
кгс/см (при 10 °С).
(при 10 °С).
Реактивные силы в холодном состоянии:
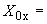 -91,5(-1·2,12·10
-91,5(-1·2,12·10 /1,74·10
/1,74·10 )=111 кгс;
)=111 кгс;
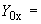 156,6(-1·2,12·10
156,6(-1·2,12·10 /1,74·10
/1,74·10 )=-191 кгс;
)=-191 кгс;
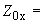 -180,3(-1·2,12·10
-180,3(-1·2,12·10 /1,74·10
/1,74·10 )=220 кгс.
)=220 кгс.
Результирующее усилие 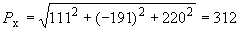 кгс.
кгс.
На черт.4 представлены эпюры составляющих момента  ,
,  ,
, 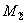 . Видно, что из прямолинейных отрезков наиболее нагружены сечения 1-го и 7-го, а из криволинейных - 2-го и 6-го. В табл.8 дается сопоставление моментов в наиболее нагруженных сечениях трубопровода.
. Видно, что из прямолинейных отрезков наиболее нагружены сечения 1-го и 7-го, а из криволинейных - 2-го и 6-го. В табл.8 дается сопоставление моментов в наиболее нагруженных сечениях трубопровода.
Таблица 8
|
Номер отрезка |
|
|
|
|
|
1 |
620 |
254 |
123 |
681 |
|
2 |
536 |
189 |
138 |
586 |
|
6 |
558 |
64 |
324 |
650 |
|
7 |
558 |
90 |
359 |
671 |
Видно, что оценка прочности должна быть произведена для отрезков 1 и 6.
Площадь поперечного сечения трубы 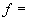 62 см
62 см . Поскольку реактивные силы
. Поскольку реактивные силы 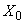 ,
, 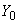 и
и 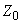 малы, можно принять, что на отрезке 1 осевая сила
малы, можно принять, что на отрезке 1 осевая сила 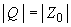 , а на отрезке 6 -
, а на отрезке 6 - 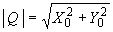 .
.
Толщина стенки рассматриваемого трубопровода удовлетворяет требованиям ОСТ 108.031.02-75. Поэтому овальность колен при определении напряжений не учитываем. Поскольку для колен 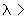 1 и
1 и 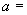 0, для определения напряжений используем только формулу (8) РТМ. Расчет производим только для отрезка 1. Получим
0, для определения напряжений используем только формулу (8) РТМ. Расчет производим только для отрезка 1. Получим
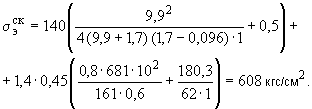
Сопоставление результатов расчета с примером 5 показывает, что точный расчет дает более низкие значения напряжений и реактивной силы от самокомпенсации.
Пример 7. Произвести ориентировочную оценку компенсирующей способности плоского разветвленного трубопровода, показанного на черт.7. Радиус колен, размеры поперечного сечения, материал и расчетные параметры рабочей среды те же, что и в трубопроводе примера 3.
Трубопровод, рассматриваемый в примере 7
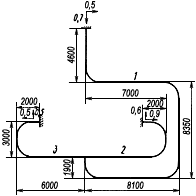
Черт.7
Для каждого из участков определяем компенсируемые перемещения  при условии, что узел перемещений не имеет, и жесткости (аналогично примеру 3). Получаем, что для участка 1
при условии, что узел перемещений не имеет, и жесткости (аналогично примеру 3). Получаем, что для участка 1 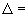 4,21 см,
4,21 см, 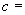 243 кгс/см, для участка 2
243 кгс/см, для участка 2 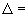 4,80 см,
4,80 см, 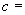 7700 кгс/см; для участка 3
7700 кгс/см; для участка 3 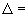 4,16 см,
4,16 см, 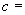 8750 кгс/см.
8750 кгс/см.
По формуле (28) РТМ определяем смещения узла применительно к каждому участку. Для участка 1 получаем
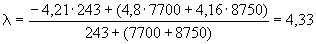 см.
см.
Аналогично находим для участка 2 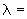 -0,02 см, для участка 3
-0,02 см, для участка 3 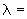 0,10 см.
0,10 см.
Определяем компенсируемые перемещения согласно п.6.2.3 РТМ.
Получаем компенсируемое перемещение для участка 1 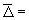 4,21+4,33=8,54 см, для участка 2
4,21+4,33=8,54 см, для участка 2 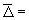 4,8-0,02=4,78 см
4,8-0,02=4,78 см , для участка 3
, для участка 3 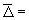 4,16+0,10=4,26 см.
4,16+0,10=4,26 см.
Реактивная сила, возникающая в участке 1 (по п.6.2.4 РТМ)
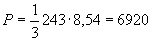 кгс;
кгс;
в участке 2
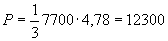 кгс;
кгс;
в участке 3
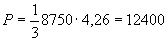 кгс.
кгс.
Оценим прочность участка 1. В примере 3 он уже рассмотрен как отдельный неразветвленный трубопровод. Коэффициент 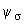 определяем аналогично примеру 3, но с уменьшением согласно п.6.2.5 РТМ в 2,5 раза; получаем
определяем аналогично примеру 3, но с уменьшением согласно п.6.2.5 РТМ в 2,5 раза; получаем 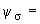 2,6/2,5=1,04. Вычисляем эквивалентное напряжение только по формуле (24), т.к. для колен трубопровода
2,6/2,5=1,04. Вычисляем эквивалентное напряжение только по формуле (24), т.к. для колен трубопровода  1 и толщина стенки удовлетворяет требованиям ОСТ 108.031.02-75. Подставляя значения величин (см. пример 3), определяем
1 и толщина стенки удовлетворяет требованиям ОСТ 108.031.02-75. Подставляя значения величин (см. пример 3), определяем

Принимая напряжения от весовой нагрузки 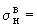 113 кгс/см
113 кгс/см (как в примере 3), устанавливаем, что условие прочности (32) РТМ при совместном действии самокомпенсации, весовой нагрузки и давления удовлетворяется:
(как в примере 3), устанавливаем, что условие прочности (32) РТМ при совместном действии самокомпенсации, весовой нагрузки и давления удовлетворяется:
-
681+113<1,5·1130.
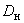
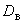
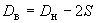 ), см;
), см;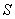
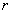
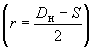 , см;
, см;
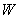
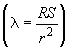 ;
;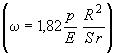 ;
;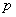
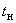
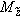
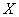 ,
, 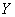 ,
, 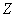
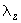
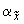 ,
, 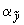 ,
, 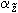
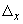 ,
, 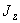
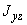 ,
, 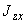
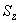
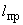
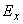
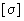
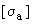
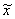 (или
(или 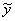 ,
, 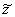 )
)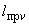 , м
, м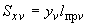
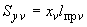
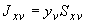
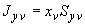
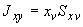
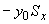
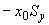
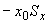
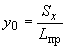 ,
, 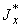
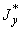
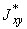
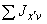
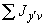
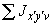
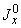
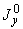
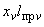 , м
, м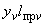 , м
, м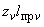 , м
, м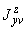 ,
,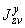
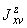 ,
,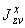
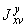 ,
,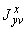
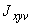
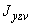
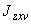
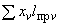
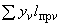
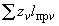
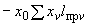
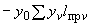
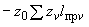
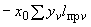
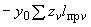
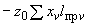
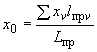 ;
; 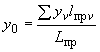 ;
; 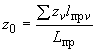 .
.
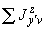 ,
, 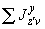
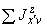 ,
, 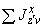
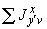 ,
, 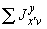
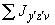
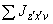
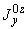 ,
, 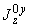
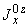 ,
, 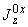
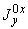 ,
, 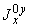
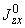
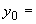 2,38
2,38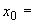 0,835
0,835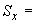 16,61
16,61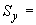 5,84
5,84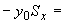 -39,5
-39,5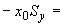 -4,88
-4,88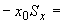 -13,9
-13,9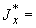 8,33
8,33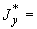 3,63
3,63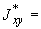 -4,5
-4,5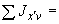 0,14
0,14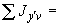 0,16
0,16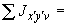 0,08
0,08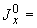 8,47
8,47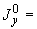 3,79
3,79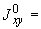 -4,42
-4,42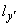
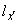
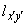
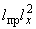 , м
, м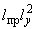 , м
, м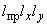 , м
, м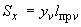
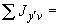 29,2
29,2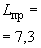
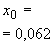
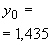
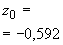
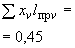
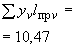
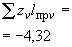
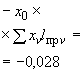
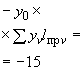
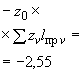
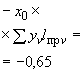
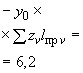
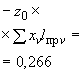
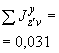
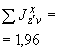
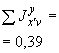
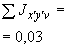
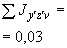
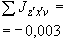
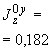
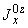 ,
,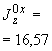
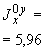
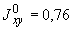
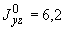
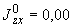
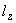 , м
, м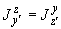
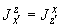
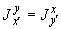
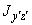
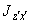
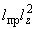 , м
, м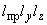 , м
, м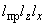 , м
, м
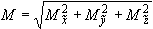 ,
,