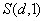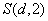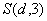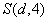РСН 67-87 Инженерные изыскания для строительства, составление прогноза изменений температурного режима вечномерзлых грунтов численными методами
 РСН 67-87
РСН 67-87
------------------------
Госстрой РСФСР
РЕСПУБЛИКАНСКИЕ СТРОИТЕЛЬНЫЕ НОРМЫ
Инженерные изыскания для строительства.
Составление прогноза изменений температурного режима
вечномерзлых грунтов численными методами
Дата введения 1988-01-01
РАЗРАБОТАНЫ производственным объединением "Стройизыскания" Госстроя РСФСР совместно с институтом Фундаментпроект Минмонтажспецстроя СССР.
Исполнители: канд. геол.-мин. наук А.И.Левкович ("Стройизыскания"), канд. геол.-мин. наук М.А.Минкин, инж. С.П.Дмитриева (Фундаментпроект), Ю.А.Попов ("Стройизыскания").
ВНЕСЕНЫ И ПОДГОТОВЛЕНЫ К УТВЕРЖДЕНИЮ производственным объединением по инженерно-строительным изысканиям ("Стройизыскания") Госстроя РСФСР.
Вводятся впервые.
УТВЕРЖДЕНЫ постановлением Государственного комитета РСФСР по делам строительства от 20 августа 1987 г. № 152
Настоящие Нормы устанавливают технические требования к производству работ по составлению прогноза изменений температурного режима грунтов для инженерно-геологического обоснования строительства новых, реконструкции и расширения действующих промышленных предприятий, зданий и сооружений, объектов сельскохозяйственного назначения, а также городов, поселков и сельских населенных пунктов на вечномерзлых грунтах.
Требования Норм не распространяются на составление прогноза для обоснования строительства гидротехнических, магистральных линейных и подземных сооружений, а также мостовых переходов.
Требованиями Норм следует руководствоваться при инженерно-геологическом обосновании строительства на участках талых грунтов, расположенных в пределах районов распространения вечномерзлых грунтов, а также при необходимости оценки динамики сезоннопромерзающего слоя в районах с сезонным промерзанием.
Составление прогноза изменения температурного режима грунтов необходимо производить в соответствии с требованиями к порядку составления прогноза мерзлотных инженерно-геологических условий, регламентированному РСН 31-83, а также с общими требованиями к прогнозу изменения инженерно-геологических условий, установленными действующими нормативными документами по изысканиям и проектированию оснований и фундаментов.
1. Общие положения
1.1. Составление прогноза изменений температурного режима грунтов является необходимым элементом инженерно-геологического обоснования строительства (реконструкции, расширения) объектов народного хозяйства в районах распространения вечномерзлых грунтов.
Составление прогноза изменения температурного режима грунтов производится изыскательской организацией при участии проектной организации-заказчика.
Участие проектной организации заключается:
-
в совместном с изыскательской организацией определении конкретных задач и вариантов прогноза;
-
в предоставлении необходимых исходных данных для каждого варианта прогноза;
-
в совместном с изыскательской организацией обсуждении результатов прогноза.
1.2. Составление прогноза изменений температурного режима грунтов производится для ограниченного определенным образом грунтового массива путем последовательного расчета температурных полей в этом массиве, соответствующих любым заданным моментам времени от начала расчета. Температурный режим (совокупность последовательных температурных полей) в грунтовом массиве рассчитывается как результат задаваемых на весь период расчета прогноза тепловых воздействий на верхней, боковых и нижней границах грунтового массива.
1.3. Расчет температурного режима грунтов производится для конкретных инженерно-геологических разрезов с учетом естественных изменений температурного режима воздуха и радиационного баланса дневной поверхности, естественных и техногенных условий теплообмена на поверхности грунтов (снежный и растительный покровы, насыпи, асфальтовые покрытия и т.п.) и техногенных источников и стоков тепла (здания и сооружения).
Расчет температурного режима грунтов производится на основе следующих данных:
-
материалов инженерно-геологических изысканий (инженерно-геологические разрезы с выделением классификационных разновидностей грунтов, физические и теплофизические свойства последних, естественные температуры грунтов и др.);
-
технического задания (пространственное размещение проектируемых объектов и проектный температурный режим в них, в том числе температурный режим в проветриваемых подпольях, вентилируемых насыпях и подвалах; при необходимости - вертикальная планировка территории; данные о заглублении проектируемых объектов, физические и теплофизические характеристики материала фундаментов, насыпей, полов и других теплоизоляционных покрытий и др.);
-
справочных материалов (температурный режим воздуха, радиационный баланс дневной поверхности, мощность и плотность снежного покрова и др.).
1.4. Расчетный срок (время) прогноза определяется расчетным сроком эксплуатации проектируемых объектов, для инженерно-геологического обоснования строительства которых составляется прогноз, и указывается в техническом задании.
Расчет прогноза может быть прекращен ранее в случаях стабилизации температурного режима грунтов в исследуемом грунтовом массиве. Под стабилизацией температурного режима в данном случае понимается наступление динамического равновесия температур в исследуемом массиве с учетом характера изменений тепловых воздействий на верхней границе массива.
1.5. Настоящие Нормы устанавливают правила расчета изменений температурного режима грунтов численным методом решения уравнения нестационарной теплопроводности с фазовыми переходами грунтовой влаги.
Прогноз составляется без учета миграции влаги, конвективного и лучистого теплообмена в грунтах.
При составлении прогноза учитываются:
-
неоднородность состава, свойств и состояния грунтов в исследуемой грунтовой области;
-
изменение соотносительных количеств льда и незамерзшей воды в диапазоне температур, принимаемых грунтами;
-
изменение граничных тепловых условий во времени и пространстве;
-
локальные источники и стоки тепла, расположенные внутри исследуемой грунтовой области.
1.6. Программа PROGNOZ имеет 5 модификаций, изложенных в п. 2.3, составлена на языке "ФОРТРАН-IV" и предназначена для использования на ЕС ЭВМ с операционной системой ОС ЕС MVT 6.1 и с памятью не менее 300 килобайт.
1.7. Пакет программ поставляется на магнитной ленте пользователя. Организация-держатель подлинника - институт "Фундаментпроект".
2. Алгоритм и структура программы
2.1. Математическая постановка задачи
Процесс распространения тепла в грунте в трехмерном пространстве описывается уравнением
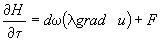 ,
,
|
где |
- |
температура грунта в точке |
|
|
- |
энтальпия (теплосодержание), отнесенная к единице объема грунта; |
|
|
- |
коэффициент теплопроводности грунта; |
|
|
- |
плотность тепловых внутренних источников и стоков в единице объема. |
Энтальпия является функцией температуры, времени и координат. Так как рассмотренные ниже выводы верны для всех точек пространства, то будем рассматривать энтальпию только как функцию температуры. С учетом теплоты фазовых переходов в грунте, энтальпия равна:
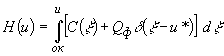 ,
,
|
где |
- |
дельта-функция Дирака |
|
|
(объемная теплоемкость талого грунта) (эффективная теплоемкость мерзлого грунта); |
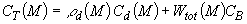 ;
;
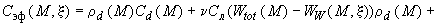
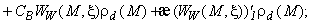
|
|
- |
удельная теплоемкость сухого грунта; |
|
|
- |
плотность сухого грунта; |
|
|
- |
удельная теплоемкость воды; |
|
|
- |
удельная теплоемкость льда; |
|
|
- |
теплота фазовых переходов; |
|
|
- |
суммарная влажность грунта в долях к весу абсолютно сухого грунта; |
|
|
- |
незамерзшая вода при температуре |
|
|
- |
коэффициенты, задающие кривую незамерзшей воды при |
Задача рассматривается в параллелепипеде 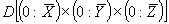 (т.е.
(т.е. 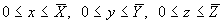 ), на гранях которого задаются краевые условия:
), на гранях которого задаются краевые условия:
на верхней границе (2)
а) температура окружающей среды:
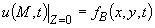
или
б) теплопоток
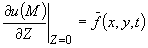
или
в) теплообмен по закону Ньютона
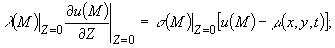
на нижней границе (3)
температура окружающей среды
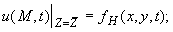 (4)
(4)
на боковых границах
постоянный теплопоток
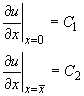
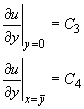
Начальная температура грунта известна во всем параллелепипеде 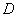 :
:

Требуется найти температуру грунта (функцию 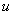 ) непрерывную в
) непрерывную в 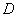 , удовлетворяющую уравнению (1), краевым условиям (2)-(4) и начальному условию (5).
, удовлетворяющую уравнению (1), краевым условиям (2)-(4) и начальному условию (5).
2.2. Алгоритм решения задачи
Предлагаемым алгоритмом задача (1)-(5) решается энтальпийным конечно-разностным методом по явной двухслойной схеме.
В прямоугольнике 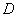 вводится произвольная прямоугольная неравномерная разностная сетка с шагами
вводится произвольная прямоугольная неравномерная разностная сетка с шагами 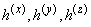 и временная сетка с шагами
и временная сетка с шагами 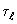 :
:
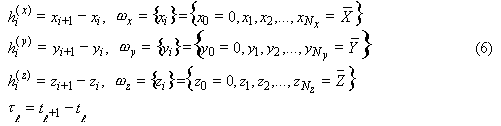
Применяя интегро-интерполяционный метод (метод баланса) построения однородных разностных схем, разностное уравнение, аппроксимирующее уравнение (1) по явной схеме на сетке (6) будет иметь вид:
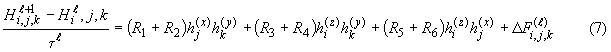
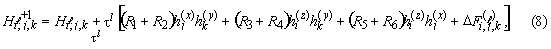
|
где |
- |
теплосодержание элемента ( |
|
|
- |
теплопоток соответственно через верхнюю, нижнюю и четыре боковые грани каждого элемента; |
|
|
- |
изменение энергии внутренних источников в объеме |
Для краевых условий I рода соответствующее 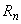 граничных элементов равны:
граничных элементов равны:
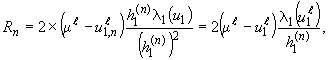
где 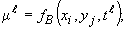
для краевых условий II рода
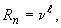
где 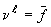 , заданная величина теплового потока;
, заданная величина теплового потока;
для краевых условий III рода
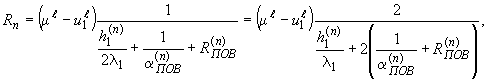
|
где |
- |
температура внешней среды; |
|
|
- |
термическое сопротивление; |
|
|
- |
коэффициент конвективного теплообмена. |
При решении задачи на шаге 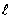 по известной температуре и энтальпии
по известной температуре и энтальпии 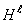 в каждом элементе определяется энтальпия на шаге
в каждом элементе определяется энтальпия на шаге 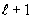 по формуле (8). Так как существует взаимно однозначное соответствие между энтальпией и температурой, то находим температуру каждого элемента на слое
по формуле (8). Так как существует взаимно однозначное соответствие между энтальпией и температурой, то находим температуру каждого элемента на слое 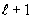 . Затем определяем энтальпию
. Затем определяем энтальпию 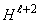 и т.д.
и т.д.
Расчетные формулы для определения энтальпии и температуры по известной энтальпии следующие:
По определению полная энтальпия
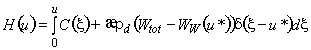 ,
,
|
где |
- |
теплоемкость грунта (рис. 1) |
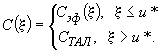
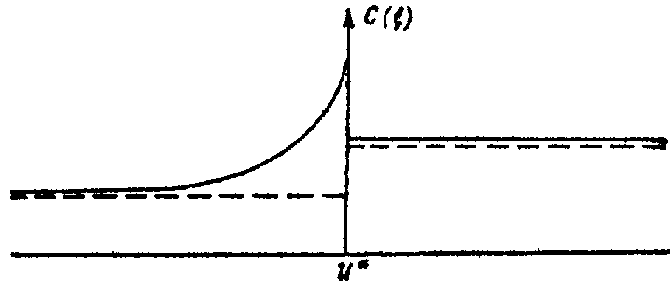
Рис. 1. График изменения теплоемкости по температуре
|
- - - - - - - - - - - |
без учета фазовых переходов в спектре отрицательных температур; |
|
____________ |
то же с учетом фазовых переходов в спектре отрицательных температур. |
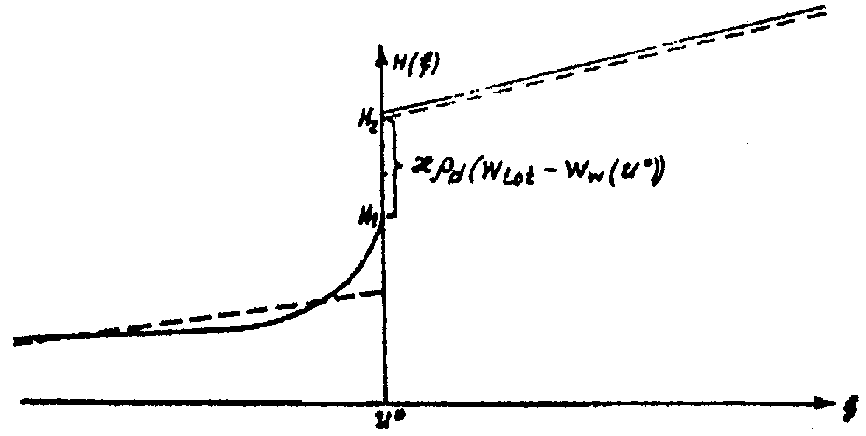
Рис. 2. График изменения энтальпии по температуре
Все дальнейшие расчеты проводятся с учетом фазовых переходов в спектре отрицательных температур. Незамерзшая вода учитывается в виде 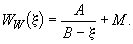
Критические значения энтальпии:
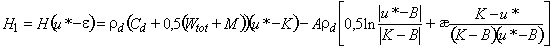 .
.
Здесь и далее 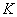 - условная температура в градусах Цельсия, при которой теплосодержание (энтальпия) принимается равной нулю. (Абсолютный нуль К=-273°С).
- условная температура в градусах Цельсия, при которой теплосодержание (энтальпия) принимается равной нулю. (Абсолютный нуль К=-273°С).
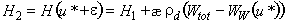 .
.
Энтальпия определяется по следующим формулам (рис. 2):
если 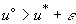 , то
, то
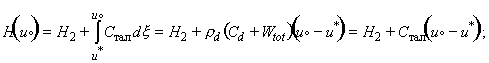
если 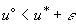 , то
, то
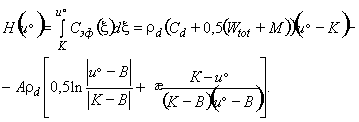
По известной энтальпии температура определяется:
если 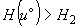 , то
, то
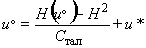 ;
;
если 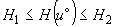 , то
, то
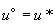 ;
;
если 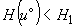 , то
, то 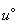 определяется линейной интерполяцией по значениям табличной функции энтальпии, составляемой для каждого слоя грунта.
определяется линейной интерполяцией по значениям табличной функции энтальпии, составляемой для каждого слоя грунта.
2.3. Структура программы
Алгоритм, описанный выше, реализован в программе PROGNOZ. Связь между частями программы представлена на рис. 3.
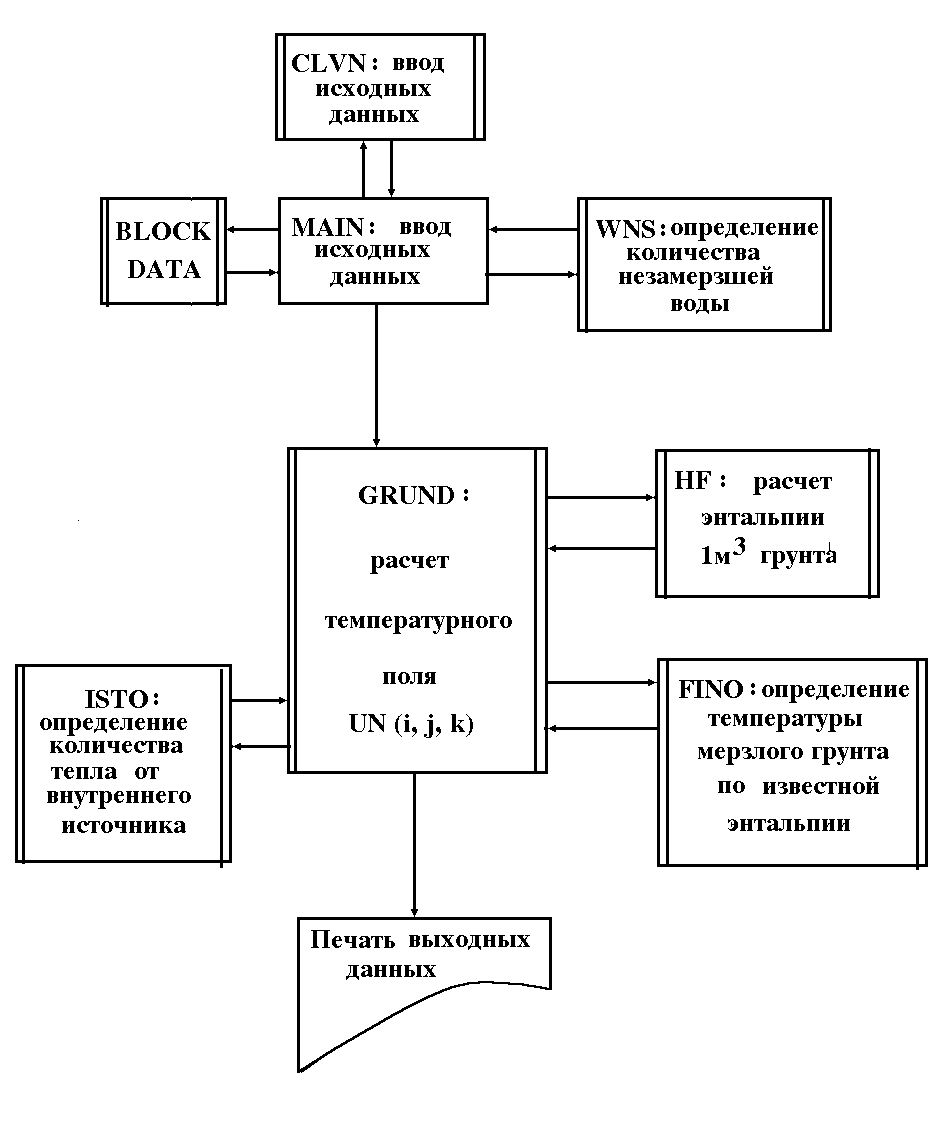
Рис. 3. Межмодульные связи в программе PROGNOZ
Программа PROGNOZ имеет 5 модификаций:
-
1. PROGNOZ -3S
Решается задача по трехмерной расчетной схеме. Главная (управляющая) программа
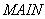 составляется для каждого варианта прогноза. В программе
составляется для каждого варианта прогноза. В программе 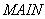 вводятся исходные массивы начальной температуры и некоторые другие исходные данные. Размерности массива, индивидуальные для каждого варианта прогноза, задаются в операторах описания.
вводятся исходные массивы начальной температуры и некоторые другие исходные данные. Размерности массива, индивидуальные для каждого варианта прогноза, задаются в операторах описания.Из программы
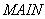 происходит обращение к подпрограмме
происходит обращение к подпрограмме 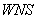 . В ней определяются коэффициенты
. В ней определяются коэффициенты 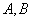 и
и 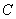 для вычисления количества незамерзшей воды в каждом слое грунта, по формуле
для вычисления количества незамерзшей воды в каждом слое грунта, по формуле 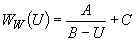 , где
, где 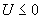 - температура грунта. Для контроля выдается на печать таблица получаемых значений
- температура грунта. Для контроля выдается на печать таблица получаемых значений 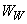 от
от 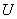 при
при 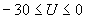 .
.Из подпрограммы
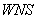 полученные массивы
полученные массивы 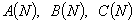 передаются в
передаются в 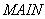 .
.В подпрограмме
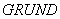 определяются одно-, двух- или трехмерные температурные поля в заданном массиве грунтов. Здесь используются подпрограмма-функция
определяются одно-, двух- или трехмерные температурные поля в заданном массиве грунтов. Здесь используются подпрограмма-функция 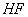 и подпрограмма
и подпрограмма 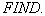
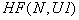 вычисляет энтальпию 1 м
вычисляет энтальпию 1 м грунта в N-ом слое при температуре
грунта в N-ом слое при температуре 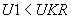 (критическая температура фазовых переходов). Для расчета функция
(критическая температура фазовых переходов). Для расчета функция 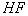 использует физико-механические и теплофизические свойства грунтов, введенные подпрограммой
использует физико-механические и теплофизические свойства грунтов, введенные подпрограммой 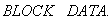
Подпрограмма
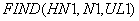 определяет температуру
определяет температуру 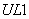 в слое грунта с номером
в слое грунта с номером 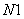 по энтальпии
по энтальпии 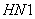 , если
, если 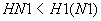 , т.е. если
, т.е. если 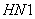 соответствует энтальпии мерзлого грунта.
соответствует энтальпии мерзлого грунта. 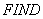 использует общую область
использует общую область 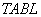 , в которой содержатся таблицы значений энтальпии по температуре от 0 до -50°С по всем грунтовым слоям, вычисленные с помощью функции
, в которой содержатся таблицы значений энтальпии по температуре от 0 до -50°С по всем грунтовым слоям, вычисленные с помощью функции 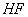 .
.Подпрограмма
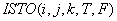 учитывает влияние источников тепла и охлаждающих установок, находящихся внутри массива грунта. Результат работы подпрограммы присваивается простой переменной
учитывает влияние источников тепла и охлаждающих установок, находящихся внутри массива грунта. Результат работы подпрограммы присваивается простой переменной 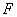 , где
, где 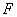 - тепло, выделяемое внутренними источниками (стоками) в единицу времени (час) в фиксированном элементе
- тепло, выделяемое внутренними источниками (стоками) в единицу времени (час) в фиксированном элементе 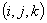 грунтового массива в момент времени
грунтового массива в момент времени  .
.Алгоритм подпрограммы может быть составлен как по экспериментальным данным, так и по теоретическим расчетам применительно к конкретному случаю.
Для обращения к подпрограмме
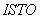 в подпрограмме
в подпрограмме 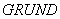 (рекомендуемое приложение 2) следует заменить оператор
(рекомендуемое приложение 2) следует заменить оператор 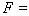
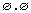 c номером 0000399 на обращение к подпрограмме
c номером 0000399 на обращение к подпрограмме 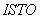 :
: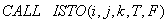 .
.В подпрограмме
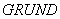 выводятся на печать значения рассчитанного температурного поля.
выводятся на печать значения рассчитанного температурного поля.Пример текста подпрограммы
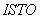 приведен в рекомендуемом приложении 2.
приведен в рекомендуемом приложении 2. -
2.
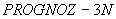
Задача решается по трехмерной расчетной схеме. Отличие от
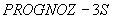 в том, что вся исходная информация вводится только с перфокарт, изменений текста не требуется. Максимальное количество элементов в расчетной области - 3000. Ввод данных осуществляется в управляющей программе
в том, что вся исходная информация вводится только с перфокарт, изменений текста не требуется. Максимальное количество элементов в расчетной области - 3000. Ввод данных осуществляется в управляющей программе 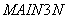 и подпрограмме
и подпрограмме 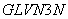 .
.Подпрограмма
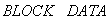 отсутствует.
отсутствует. -
3.
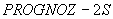
Эта подпрограмма отличается от
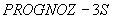 тем, что рассчитывает только двух- и одномерные температурные поля. Программа
тем, что рассчитывает только двух- и одномерные температурные поля. Программа 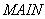 и
и 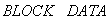 составляются для каждого варианта прогноза. Расчет двухмерных задач по модификации
составляются для каждого варианта прогноза. Расчет двухмерных задач по модификации 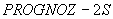 сокращает время расчета по отношению к
сокращает время расчета по отношению к 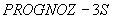 приблизительно в 1,5 раза.
приблизительно в 1,5 раза. -
4.
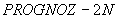
Аналогично
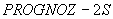 рассчитывает только двух- и одномерные температурные поля. Вся исходная информация вводится только с перфокарт. Ввод данных осуществляется в подпрограмме
рассчитывает только двух- и одномерные температурные поля. Вся исходная информация вводится только с перфокарт. Ввод данных осуществляется в подпрограмме 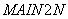 и подпрограмме
и подпрограмме 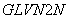 . Подпрограмма
. Подпрограмма 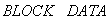 отсутствует. Максимальное количество элементов в расчетной области - 3000.
отсутствует. Максимальное количество элементов в расчетной области - 3000. -
5.
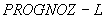
Решается двухмерная задача. Верхняя граница области исследования может быть задана ступенчатой линией.
Ввод данных аналогичен 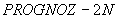 . Максимальное количество элементов (с учетом фиктивных) в расчетной области - 3000.
. Максимальное количество элементов (с учетом фиктивных) в расчетной области - 3000.
3. Подготовка исходных данных для расчета
3.1. Расчетная область
Расчетная область исследования может быть задана трехмерной, двухмерной или одномерной. Так как в грунтах теплообмен всегда пространствен, т.е. трехмерен, то в трехмерной расчетной области может решаться любая задача прогнозирования. В этом случае любая точка 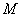 грунта определяется координатами
грунта определяется координатами 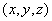 в прямоугольной системе координат. В ряде случаев задача может быть сведена к двухмерной и даже одномерной, что более выгодно и удобно при расчете на ЭВМ.
в прямоугольной системе координат. В ряде случаев задача может быть сведена к двухмерной и даже одномерной, что более выгодно и удобно при расчете на ЭВМ.
Алгоритм составлен и может быть применен для расчетных областей, ограниченных прямоугольной верхней границей, в контурах которой фиксированы в плане тепловыделяющие объекты. В трехмерном случае область исследования параллелепипед, в двухмерном - прямоугольник и в одномерном - прямая. Для создания объема в двухмерной и одномерной областях задаются по направлениям, в которых размеры не определяются, единичные размеры, равные 1 м.
Область исследования фиксируется прямоугольной системой координат, с центром 0 в одной из вершин параллелепипеда и направлением осей:  - в вертикальном направлении,
- в вертикальном направлении,  и
и  - в горизонтальных. Направление горизонтальных осей
- в горизонтальных. Направление горизонтальных осей  и
и  совпадает с осевыми линиями тепловыделяющих объектов. Величина ребер параллелепипеда определяет размеры области исследования. Его грани являются границами области исследования.
совпадает с осевыми линиями тепловыделяющих объектов. Величина ребер параллелепипеда определяет размеры области исследования. Его грани являются границами области исследования.
Различаются верхняя, нижняя и четыре боковые границы (соответственно верхняя, нижняя и четыре боковые грани параллелепипеда).
Теплопоток через боковые границы области исследования должен быть постоянен во времени и по всей плоскости грани. Исходя из этого, определяются размеры области исследования.
На практике чаще применяется условие отсутствия теплопотока через боковые границы. Тогда для тепловыделяющих сооружений расстояние от их контура в плане до боковой границы области исследования должно быть в 2,5-3 раза больше, чем размеры самого здания в том же направлении.
Положение нижней границы (глубина области исследования) выбирается ниже глубины распространения годовых колебаний температуры в грунтах и зависит от интенсивности тепловыделения на верхней границе, а также срока прогнозного расчета.
При естественных условиях теплообмена на верхней границе, или без наличия тепловыделяющих сооружений эта глубина должна быть не менее 15-20 м. В остальных случаях она должна быть на 10 м больше максимальной глубины чаши оттаивания, определенной расчетом по СНиП II-18-76.
При определении области исследования следует исходить также из экономии времени счета на ЭМВ. Для этого следует использовать возможную симметричность задачи, а также возможность сведения трехмерной области с двухмерной или одномерной.
Если задача симметрична или может быть сведена к симметричной, то в трехмерной задаче плоскость (или плоскости) симметрии, а в двухмерной ось (или оси) симметрии должны быть границами области исследования с условием отсутствия теплообмена на них.
3.2. Разбивка области исследования
Область исследования разбивается на прямоугольные элементы произвольных размеров (рис. 4).
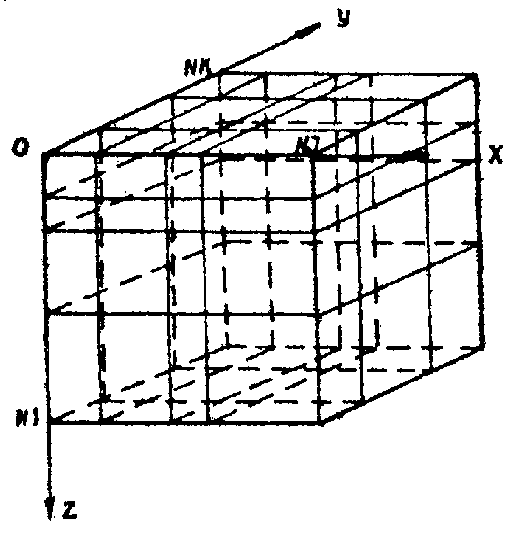
Рис.4. Пример разбивки области исследования
Разбивка производится горизонтальными и вертикальными плоскостями (разбивочными плоскостями), параллельными соответствующим границам области в следующем порядке:
-
на верхней и нижней границах области исследования выделяются зоны с различным режимом теплообмена грунта с окружающей средой. На каждой из этих границ может быть выделено до 9 таких зон;
-
границы выделенных зон с различным режимом теплообмена должны быть параллельны боковым границам области исследования. Если граница выделенной зоны не отвечает этому требованию, то она заменяется ступенчатой линией со "ступеньками", аппроксимирующими ее контур и удовлетворяющими указанному требованию;
-
после построения границ зон через каждую прямую, образующую "ступеньки", как на верхней, так и на нижней границах области исследования проводятся разбивочные плоскости;
-
криволинейные границы литологических разностей заменяются ступенчатыми, с плоскостями образующих их "ступенек", параллельными границам области исследования;
-
проводятся разбивочные плоскости через плоскости полученных "ступенек";
-
проводятся остальные разбивочные плоскости так, чтобы в зоне возможных фазовых переходов грунтовой влаги размеры ребер получаемых прямоугольных элементов в направлении теплообмена составляли от 0,5 до 2 м. Размер ребер тех же элементов в перпендикулярных направлениях может быть соответственно в 2-3 раза больше. Вне зоны возможных фазовых переходов и влияния тепловыделяющих объектов размер элементов в направлении теплообмена может быть постепенно увеличен до 6-8 м.
По каждому направлению число элементов не должно превышать 100.
В результате проведенного разбиения область исследования состоит из прямоугольных элементов разных размеров. Каждая выделенная литологическая разность представлена целым числом элементов. В контурах зон с различным режимом теплообмена на верхней и нижней границах содержится целое число элементов (в плане).
Полученное разбиение остается постоянным на все время проведения расчета.
За каждым элементом закрепляется трехзначный индекс 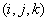 , где
, где  определяет номер элемента по направлению оси
определяет номер элемента по направлению оси  ,
,  - по направлению оси
- по направлению оси  и
и 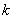 - по направлению оси
- по направлению оси  .
.
Фиксируется число расчетных элементов по направлению осей.
Обозначим их соответственно 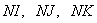 . Произведение
. Произведение 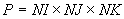 определяет число расчетных элементов во всей области исследования.
определяет число расчетных элементов во всей области исследования.
При решении двухмерной задачи 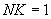 . При решении одномерной
. При решении одномерной 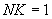 и
и 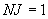 .
.
3.3. Начальные условия
В каждом полученном элементе области исследования задаются начальные условия 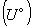 , т.е. температуры грунта, соответствующие времени начала расчета. Эти температуры назначаются в геометрических центрах элементов и считается, что каждый элемент характеризуется температурой его центра. Последнее положение также относится к любым температурным полям, полученным в процессе расчета задачи.
, т.е. температуры грунта, соответствующие времени начала расчета. Эти температуры назначаются в геометрических центрах элементов и считается, что каждый элемент характеризуется температурой его центра. Последнее положение также относится к любым температурным полям, полученным в процессе расчета задачи.
Начальное распределение температур в области исследований назначается по данным термокаротажных работ. Время проведения этих работ считается моментом начала расчета.
Начальная температура 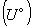 ни в одном из элементов не может назначаться равной температуре начала фазовых переходов
ни в одном из элементов не может назначаться равной температуре начала фазовых переходов 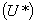 . В этом случае задается температура
. В этом случае задается температура 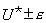 , где
, где 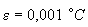 .
.
Начальная температура грунта 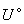 записывается в табл. 1 по "разрезам", сделанным параллельно оси
записывается в табл. 1 по "разрезам", сделанным параллельно оси  области исследования для каждого фиксированного значения
области исследования для каждого фиксированного значения 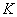 , где
, где 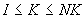 .
.
Таблица 1
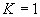
|
i \ j |
|
|
|
|
|
|
U(1, 1, 1) |
U(1, 2, 1) . . . . . . . . |
U(1, NJ, 1) |
|
|
|
U(2, 1, 1) |
U(2, 2, 1) . . . . . . . . |
U(2, NJ, 1) |
|
|
|
U(3, 1, 1) |
U(3, 2, 1) . . . . . . . . |
U(3, NJ, 1) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
|
U(Ni, 1, 1) |
U(1, 2, 1) |
. . . . . . . . |
U(Ni, NJ, 1) |
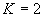
|
i \ j |
j=1 |
j=2 |
j=J |
|
|
|
U(1, 1, 2) |
U(1, 2, 2) . . . . . . . . |
U(1, NJ, 2) |
|
|
|
U(2, 1, 2) |
U(2, 2, 2) . . . . . . . . |
U(2, NJ, 2) |
|
|
|
U(3, 1, 2) |
U(3, 2, 2) . . . . . . . . |
U(3, NJ, 2) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
i=Ni |
(Ni, 1, 2) |
(Ni, 2,2) |
. . . . . . . . |
(Ni, NJ, 2) |
и т.д.
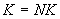
|
i \ j |
j=1 |
j=2 |
j=J |
|
|
|
U(1, 1, NK) |
U(1, 2, NK). . . . . . . . |
U(1, NJ, NK) |
|
|
|
U(2, 1, NK) |
U(2, 2, NK) . . . . . . . . |
U(2, NJ, NK) |
|
|
|
U(3, 1, NK) |
U(3, 2, NK) . . . . . . . . |
U(3, NJ, NK) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
i=Ni |
U(Ni, 1, NK) |
U(Ni, 2, NK) |
. . . . . . |
U(Ni, NJ, NK) |
3.4. Граничные условия
Граничные условия задаются на каждой границе области исследований на все время расчета температурного режима.
На верхней границе области исследования задаются независимые друг от друга граничные условия в каждой выделенной зоне с различным режимом теплообмена грунта с внешней средой.
Количество граничных условий на нижней границе определяется количеством выделенных на границе зон с различным режимом теплообмена. В одномерных задачах на верхней и нижней границах задается только одно граничное условие.
На каждой из боковых границ области исследования задается по одному граничному условию.
Различают граничные условия I, II и III рода.
Условие I рода - известна температура грунта на поверхности границы.
Условие II рода - известен теплопоток через поверхность границы.
Условие III рода - теплообмен через границу области исследования определятся температурой окружающей среды и коэффициентом теплообмена, т.е. происходит по закону Ньютона.
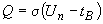 ,
,
|
где |
- |
количество приходящего к поверхности грунта или уходящего от него тепла, кДж (ккал); |
|
|
|
- |
коэффициент теплоотдачи с поверхности грунта, |
|
|
Вт/ |
ккал/ |
||
|
|
- |
температура поверхности грунта, |
|
|
|
- |
температура окружающей среды, |
|
Граничные условия верхней границы изменяются с периодом повторения 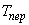 , назначаемым в исходных данных расчета. На практике наиболее часто употребляется
, назначаемым в исходных данных расчета. На практике наиболее часто употребляется 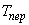 - 1 год = 8760 часов.
- 1 год = 8760 часов.
Период счета разбит на интервалы. Если период год, то интервалов 12 (12 месяцев) или 36 (36 декад). Количество интервалов задается в исходных данных переменной 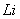 . На верхней границе области исследования, в каждой выделенной зоне с различным режимом теплообмена грунта с внешней средой, для каждого интервала периода счета задаются следующие средние значения за этот интервал величин, определяющих теплообмен в зависимости от рода краевых условий в зоне:
. На верхней границе области исследования, в каждой выделенной зоне с различным режимом теплообмена грунта с внешней средой, для каждого интервала периода счета задаются следующие средние значения за этот интервал величин, определяющих теплообмен в зависимости от рода краевых условий в зоне:
-
для условий I рода задается температура поверхности грунта,
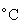 ;
; -
для условий II рода задается величина теплопотока, кДж (ккал);
для условий III рода задаются:
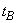
-
температура окружающей среды,
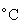 ;
;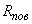
-
термическое сопротивление поверхности грунта,
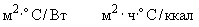 ;
;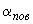
-
коэффициент теплообмена,
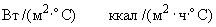 .
.
На любой момент времени от начала счета значения этих величин определяются линейной интерполяцией между значениями их в соседних интервалах.
На нижней границе задаются условия теплообмена I рода. При этом в каждой выделенной зоне значения температуры могут быть только постоянными на все время проведения расчета.
На каждой из 4-х боковых границ задаются условия II рода. Теплопоток на каждой границе постоянен на все время проведения расчета и по всей плоскости грани. Для граничных условий верхней границы заполняется табл. 2. При этом каждой выделенной зоне присваивается постоянный номер от 1 до 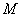 , где
, где 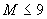 .
.
Таблица 2
|
Номер зоны |
Род краевых условий |
характеристики |
месяц (или декада) I II III IV . . .XII |
|
I |
III |
Температура окружающей среды |
|
|
Термическое сопротивление |
|||
|
Коэффициент теплообмена |
|||
|
2 |
I |
Температура на поверхности грунта |
|
|
3 |
II |
Теплопоток |
|
|
4 |
III |
Температура окружающей среды |
|
|
Термическое сопротивление |
|||
|
Коэффициент теплообмена |
и т.д. для каждой выделенной зоны.
После закрепления номеров за каждой зоной краевых условий верхней границы заполняется табл. 3. Каждое значение 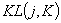 этой таблицы имеет вид:
этой таблицы имеет вид:
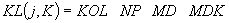 ,
,
|
где |
|
если во всех элементах если внутренние источники присутствуют хотя бы в одном из элементов |
|||
|
|
- |
номер типа источника, |
|||
|
MD |
- |
номер зоны краевых условий верхней границы, в которой находится элемент |
|||
|
MDK |
- |
номер зоны краевых условий нижней границы для соответствующего элемента |
|||
Для двухмерной задачи табл. 3 состоит из одного столбца для 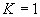 , для одномерной из одного числа
, для одномерной из одного числа 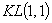 .
.
Таблица 3
|
j \ К |
|
|
|
|
|
j=1 |
KL(1, 1) |
KL(1, 2) . . . . . . . . |
KL(1, NK) |
|
|
j=2 |
KL(2, 1) |
KL(2, 2) . . . . . . . . |
KL(2, NK) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
j=NJ |
KL(NJ, 1) |
KL(NJ, 2) |
. . . . . . . |
KL(NJ, NK) |
3.5. Физические и теплофизические свойства
Расчетная область может содержать до 10 литологических разностей, характеризующихся следующими свойствами, учитывающимися алгоритмом:
|
где |
- |
плотность сухого грунта кг/куб.м; |
|
|
- |
весовая влажность грунта, доли единицы; |
|
|
- |
удельная теплоемкость скелета, |
|
|
- |
коэффициент теплопроводности грунта в талом состоянии |
|
|
- |
коэффициент теплопроводности грунта в мерзлом состоянии |
|
|
- |
температура начала фазовых переходов, |
|
|
- |
количество незамерзшей воды в диапазоне отрицательных температур, доли, задаваемой кривой |
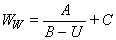 ,
,
|
где А, В, С |
- |
коэффициенты, определяющие количество незамерзшей воды в данной литологической разности. |
Все вышеуказанные свойства должны быть определены для каждой литологической разности по лабораторным данным, справочным или нормативным документам. Они остаются неизменными для всего времени счета.
Составляется табл. 4. При этом каждой литологической разности присваивается постоянный номер от 1 до 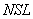 , где
, где 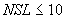 .
.
Таблица 4
|
Номер литологи- ческой разности |
|
|
|
|
|
|
|
|
1 |
|||||||
|
2 |
|||||||
|
и т.д. |
|||||||
В графе 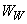 помещается информация о незамерзшей воде в данном слое. Если известна кривая, то есть уже известны коэффициенты
помещается информация о незамерзшей воде в данном слое. Если известна кривая, то есть уже известны коэффициенты 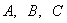 ее задающие, то записываются значения коэффициентов. Если известны лабораторные данные, то приводятся они. Например:
ее задающие, то записываются значения коэффициентов. Если известны лабораторные данные, то приводятся они. Например: 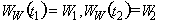 и так далее не менее трех значений. Если в расчете
и так далее не менее трех значений. Если в расчете 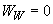 , то коэффициенты, задающие кривую незамерзшей воды в данном слое, будут равны:
, то коэффициенты, задающие кривую незамерзшей воды в данном слое, будут равны: 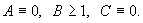
После закрепления номеров за каждой литологической разностью заполняется табл. 5, структура которой повторяет табл. 1. Таблицей 5 за каждым элементом 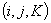 , полученным при разбивке области исследования, закрепляется номер той литологической разности, которой он принадлежит.
, полученным при разбивке области исследования, закрепляется номер той литологической разности, которой он принадлежит.
Таблица 5
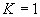
|
i \ j |
j=1 |
j=2 . . . . . . . . |
j=NJ |
|
|
|
N(1, 1, 1) |
N(1, 2, 1) . . . . . . . . |
N(1, NJ, 1) |
|
|
|
N(2, 1, 1) |
N(2, 2, 1) . . . . . . . . |
N(2, NJ, 1) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
i=Ni |
N(Ni, 1, 1) |
N(Ni, 2, 1) |
N(Ni, NJ, 1) |
|
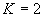
|
i \ j |
j=1 |
j=2 . . . . . . . . |
j=NJ |
|
|
|
N(1, 1, 2) |
N(1, 2, 2) |
N(1, NJ, 2) |
|
|
|
N(2, 1, 2) |
N(2, 2, 2) |
N(2, NJ, 2) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
i=Ni |
N(Ni, 1, 2) |
N(Ni, 2, 2) |
N(Ni, NJ, 2) |
|
и т.д.
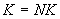
|
i \ j |
j=1 |
j=2 . . . . . . . . . . |
j=NJ |
|
|
|
N(1, 1, K) |
N(1, 2, K) . . . . . . . . |
N(1, NJ, NK) |
|
|
|
N(2, 1, K) |
N(2, 2, K) . . . . . . . . |
N(2, NJ, NK) |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
. |
. |
. |
. |
|
|
i=Ni |
N(Ni, 1, K) |
N(Ni, 2, K) |
N(Ni, NJ, NK) |
|
Каждое значение 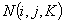 в табл. 5 может быть только целым числом от 1 до
в табл. 5 может быть только целым числом от 1 до 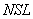 , где
, где 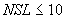 - число выделенных литологических разностей.
- число выделенных литологических разностей.
3.6. Дополнительные данные, необходимые для проведения расчета
Для проведения расчета необходимо также определить значение следующих величин, задействованных алгоритмом.
Шаг по времени. Размеры элементов и шаг по времени связаны между собой следующим соотношением:
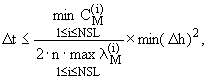
|
где |
- |
шаг по времени, ч; |
|
|
- |
номер грунтовой разности; |
|
|
- |
число выделенных грунтовых разностей; |
|
|
- |
теплоемкость мерзлого грунта |
|
|
- |
количество незамерзшей воды, доли; |
|
|
- |
плотность сухого грунта, |
|
|
- |
удельная теплоемкость сухого грунта, |
|
|
- |
удельная теплоемкость льда, |
|
|
- |
коэффициент объемного расширения, |
|
|
- |
весовая влажность грунта, доли; |
|
|
- |
коэффициент теплопроводности мерзлого грунта, |
|
|
- |
мерность области исследования, |
|
|
- |
размер ребра элемента. |
Шаг по времени может быть изменен в процессе счета 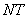 раз, где
раз, где 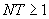 .
.
Время изменения расчетного шага от начала расчета задается одномерным массивом 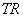 размерностью
размерностью 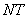 .
.
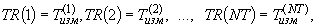
|
где |
- |
время изменения шага от начала счета в часах. |
Отсчет происходит от момента начала счета, т.е. от 0.
Определяется 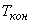 (час) - время окончания решения задачи. Задаются
(час) - время окончания решения задачи. Задаются 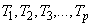 - время выдачи результатов расчета на печать (в часах). Время последней выдачи результата
- время выдачи результатов расчета на печать (в часах). Время последней выдачи результата 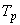 обязательно меньше
обязательно меньше 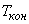 на один шаг по времени. В противном случае счет может прекратиться раньше, чем будет получен последний результат.
на один шаг по времени. В противном случае счет может прекратиться раньше, чем будет получен последний результат.
Определяются интервалы, через которые происходит очередная выдача результатов на печать.
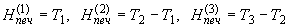 и т.д.
и т.д.
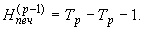
Для последующего ввода в ЭВМ формируется одномерный массив HPRI размерностью INT. Размерность INT массива зависит от того, с постоянным шагом выдаются результаты расчета или нет.
|
|
- - |
выдача производится с постоянным шагом; выдача производится с переменным шагом. |
Если INT = 2, то 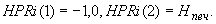
Если INT = Р+1, то  и т.д.
и т.д. 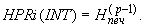
Задание печати распределения температур
Для удобства обработки информации, получаемой в результате расчета, фиксируются необходимые для анализа температурного режима "линии разрезов", по которым выдается на печать распределение температур.
Положение "разрезов", параллельных плоскости 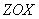 , задается координатой
, задается координатой 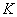 элементов, составляющих этот разрез.
элементов, составляющих этот разрез.
Формируется массив целых чисел 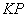 размерностью
размерностью 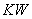 , где
, где 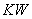 - число выдаваемых на печать "разрезов" по направлению
- число выдаваемых на печать "разрезов" по направлению 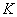 . Если по этому направлению ни одного разреза выдавать на печать не надо, то
. Если по этому направлению ни одного разреза выдавать на печать не надо, то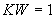 и
и 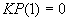 . В противном случае
. В противном случае 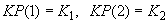 и т.д.
и т.д. 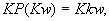 где
где 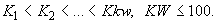
Положение “разрезов”, параллельных плоскости 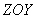 , задается координатой
, задается координатой  элементов, составляющих этот разрез.
элементов, составляющих этот разрез.
Формируется массив целых чисел 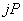 размерностью
размерностью 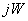 , где
, где 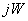 - число выдаваемых на печать “разрезов” по направлению j. Если по этому направлению ни одного разреза выдавать на печать не надо, то
- число выдаваемых на печать “разрезов” по направлению j. Если по этому направлению ни одного разреза выдавать на печать не надо, то 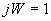 и
и 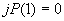 . В противном случае
. В противном случае 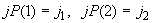 и т.д.
и т.д. 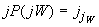 , где
, где 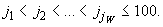
Положение "разрезов", параллельных плоскости 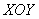 , задается координатой
, задается координатой  элементов, составляющих этот разрез.
элементов, составляющих этот разрез.
Формируется массив целых чисел 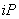 размерностью
размерностью 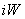 , где
, где 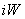 - число выдаваемых на печать "разрезов" по направлению
- число выдаваемых на печать "разрезов" по направлению  .
.
Если по этому направлению ни одного разреза выдавать на печать не надо, то 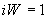 и
и 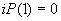 . В противном случае
. В противном случае 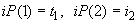 и т.д.
и т.д. 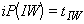 , где
, где 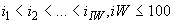 .
.
4. Проведение расчета
4.1. Вызов и загрузка программы в ЭВМ
Каждая из модификаций программы 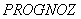 состоит из нескольких модулей, объединенных главной программой
состоит из нескольких модулей, объединенных главной программой 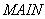 . Подпрограммы-модули
. Подпрограммы-модули 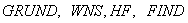 содержатся в личной библиотеке исходных модулей (или библиотеке загрузочных модулей).
содержатся в личной библиотеке исходных модулей (или библиотеке загрузочных модулей).
Ниже приводится пример пакета вызова программы 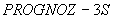 из библиотеки исходных модулей. Задание требует не менее 300 килобайт памяти и использует оптимизирующий транслятор (ФОРТРАН-011) системы
из библиотеки исходных модулей. Задание требует не менее 300 килобайт памяти и использует оптимизирующий транслятор (ФОРТРАН-011) системы 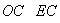 .
.
Здесь:
имя - биб - имя личной библиотеки исходных модулей,
имя - тома - имя тома, на котором размещена библиотека.
|
// |
JOB |
||
|
// |
EXEC |
FORTHCLG |
|
|
// |
FORT. |
SYSIN DD DDNAME=PKAR |
|
|
// |
DD |
DSN=<ИМЯ-БИБ>(GRUND),DISP=SHR, |
|
|
// |
VOL=SER=<ИМЯ-ТОМА>,UNIT=SYSDA |
||
|
// |
DD |
DSN=<ИМЯ-БИБ>(WNS),DISP=SHR, |
|
|
// |
VOL=SER=<ИМЯ-ТОМА>,UNIT=SYSDA |
||
|
// |
DD |
DSN=<ИМЯ-БИБ>(HF), DISP=SHR, |
|
|
// |
VOL=SER=<ИМЯ-ТОМА>,UNIT=SYSDA |
||
|
// |
DD |
DSN=<ИМЯ-БИБ>(FIND), DISP=SHR, |
|
|
// |
VOL=SER=<ИМЯ-ТОМА>,UNIN=SYSDA |
||
|
// |
PKAP |
DD* |
|
|
<текст программы MAIN на перфокартах> |
|||
|
<текст подпрограммы BLOCK DATA на перфокартах> |
|||
|
// |
GО. |
SYSIN DD* |
|
|
<исходные данные> |
|||
|
/* |
|||
|
// |
|||
Текст подпрограмм для модификации 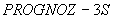 приведен в обязательном приложении 3.
приведен в обязательном приложении 3.
4.2. Составление программы 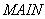 и подпрограммы
и подпрограммы 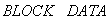
Программа 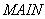 в модификациях
в модификациях 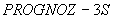 и
и 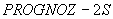 составляется для каждого варианта расчета. Пример программы
составляется для каждого варианта расчета. Пример программы 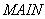 для расчета контрольного примера (приложение 1) приведен в обязательном приложении 3.
для расчета контрольного примера (приложение 1) приведен в обязательном приложении 3.
Программа 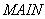 содержит обращение к основной подпрограмме
содержит обращение к основной подпрограмме 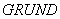 алгоритма. Перед обращением к подпрограмме
алгоритма. Перед обращением к подпрограмме 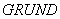 в
в 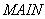 должны быть определены все формальные аргументы подпрограммы, приведенные в табл. 6.
должны быть определены все формальные аргументы подпрограммы, приведенные в табл. 6.
Таблица 6
|
Идентификатор |
Фактическое значение |
|
1 |
2 |
|
|
|
|
|
Число элементов по направлению |
|
|
Число элементов по направлению |
|
|
Число элементов по направлению |
|
NT |
Число изменений шага по времени |
|
LI |
Число интервалов времени в периоде, во время которых задаются средние значения характеристик внешней среды на верхней границе |
|
|
Число зон с различными краевыми условиями на верхней границе |
|
|
Число зон с различными краевыми условиями на нижней границе |
|
|
Время окончания счета (в часах) |
|
|
Одномерные массивы размерности |
|
|
Коэффициенты, задающие кривую незамерзшей воды по слоям |
|
|
Трехмерный массив размерностью |
|
|
Двухмерный массив размерностью |
|
U(NI, NJ, NK) |
Трехмерный массив размерностью |
|
|
Число выдаваемых на печать "разрезов" по направлению |
|
|
Число выдаваемых на печать "разрезов" по направлению |
|
|
Число выдаваемых на печать "разрезов" по направлению |
|
|
Размер массива |
|
|
Одномерный массив размерности |
|
|
Трехмерный массив размерностью Значение энтальпии по элементам на текущем временном слое |
|
|
Трехмерный массив размерностью |
|
|
Трехмерный массив размерностью |
|
|
|
|
|
Оператором 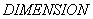 определяется размерность массивов
определяется размерность массивов 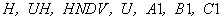 . Ввод массивов
. Ввод массивов 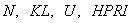 осуществляется операторами описания типа
осуществляется операторами описания типа 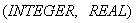 , а также операторами присваивания.
, а также операторами присваивания.
Применение операторов описания типа для ввода указанных массивов, в подавляющем большинстве проводимых на практике расчетов, уменьшает количество информации, вводимой с перфокарт.
Обращение к подпрограмме 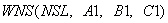 присутствует в том случае, если коэффициенты
присутствует в том случае, если коэффициенты 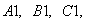 определяющие кривую незамерзшей воды по грунтовым разностям, неизвестны. В противном случае эти коэффициенты вводятся операторами присваивания или операторами описания типа.
определяющие кривую незамерзшей воды по грунтовым разностям, неизвестны. В противном случае эти коэффициенты вводятся операторами присваивания или операторами описания типа.
Обращение к подпрограмме 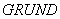 присутствует обязательно и имеет вид:
присутствует обязательно и имеет вид:
CALL GRUND (NSL, Ni, NJ, NK, NT, LI, M, M1, TKON, A1, B1, C1,
N, KL, U, IW, JW, KW, INT, HPRI, H, UN, HNOV, NSi).
Простые переменные NSL, NI, NJ, NK, NT, LI, M, M1, TKON, IW, JW, KW, INT, NSi при обращении к подпрограмме заменяются своими фактическими значениями (см. табл. 6).
Массивы 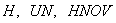 определяются только размерностью в операторе
определяются только размерностью в операторе 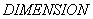 .
.
В подпрограмме 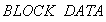 (см. приложение 3) оператором
(см. приложение 3) оператором 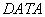 вводятся значения по слоям следующих физических и теплофизических характеристик грунта соответствующими идентификаторами:
вводятся значения по слоям следующих физических и теплофизических характеристик грунта соответствующими идентификаторами:
|
|
- |
плотность сухого грунта, |
|
|
- |
удельная теплоемкость сухого грунта, |
|
|
- |
суммарная влажность грунта в долях к весу абсолютно сухого грунта (доли); |
|
|
- |
температура начала фазовых переходов. |
Значения характеристик берутся из табл. 4.
Текст программы 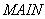 и подпрограммы
и подпрограммы 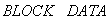 записывается на стандартных бланках для записи текста на
записывается на стандартных бланках для записи текста на 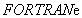 с последующей набивкой на перфокарты.
с последующей набивкой на перфокарты.
4.3. Подготовка к вводу группы данных с перфокарт
Начальные данные, вводимые с перфокарт, описаны в порядке ввода в табл. 7 и 8.
Таблица 7
|
Поряд- |
Идентификатор |
Формат |
Единица измерения |
Значение |
|
1 |
|
|
|
|
|
2 |
|
|
доли ед. |
Соответствующее указанным выше температурам количество незамерзшей воды |
Таблица 8
|
Поряд- |
Идентификатор |
Формат |
Единица измерения |
Значение |
|
1 |
2 |
3 |
4 |
5 |
|
3 |
|
|
|
|
|
|
|
Одномерный массив размерностью |
||
|
|
м |
Одномерный массив размерностью |
||
|
|
м |
Одномерный массив размерностью |
||
|
|
м |
Одномерный массив размерностью |
||
|
|
ч |
Одномерный массив размерностью |
||
|
4 |
|
|
ч |
Одномерный массив размерностью |
|
5 |
|
|
|
Двухмерный массив размерностью |
|
RB(LI, M) |
|
Двухмерный массив размерностью |
||
|
AB(LI, M) |
|
Двухмерный массив размерностью |
||
|
TBIK(M1) |
|
Одномерный массив размерностью |
||
|
TBJ |
|
Простая переменная. Теплопоток на левой боковой границе области исследования |
||
|
TBJK |
|
Простая переменная. Теплопоток на правой боковой границе |
||
|
TBK |
|
Простая переменная. Теплопоток на ближней боковой границе |
||
|
TBKK |
|
Простая переменная. Теплопоток на дальней боковой границе |
||
|
6 |
MR(M) |
2713 |
б/р |
Одномерный массив размерностью |
|
MK(5) |
б/р |
Одномерный массив размерностью 5. Род краевых условий соответственно по нижней, ближней, дальней, левой и правой границах |
||
|
JP(JW) |
б/р |
Одномерный массив размерностью |
||
|
KP(KW) |
б/р |
Одномерный массив размерностью |
||
|
IP(IW) |
б/р |
Одномерный массив размерностью |
По табл. 7 вводятся данные, необходимые для расчета коэффициентов кривой незамерзшей воды подпрограммой 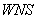 , для каждой выделенной грунтовой разности. Если в программе
, для каждой выделенной грунтовой разности. Если в программе 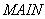 обращения к подпрограмме
обращения к подпрограмме 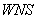 нет, то числовые данные для ввода готовятся только по табл. 8.
нет, то числовые данные для ввода готовятся только по табл. 8.
Все переменные, соответствующие одному порядковому номеру оператора ввода, вводятся по единому формату.
4. 4. Выходные данные
При работе программы за каждый шаг расчета по времени обновляется трехмерный массив температур 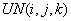 , содержащий значения температур в центрах элементов исследуемого массива грунта. На заданный в исходных данных (п. 3.6) момент времени может быть выведено на печать двухмерное температурное поле, представляющее собой разрез массива
, содержащий значения температур в центрах элементов исследуемого массива грунта. На заданный в исходных данных (п. 3.6) момент времени может быть выведено на печать двухмерное температурное поле, представляющее собой разрез массива 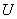 , определенный исходными параметрами (см. п. 3.6). Если в некотором элементе происходят фазовые переходы, то есть температура грунта равна температуре начала фазовых переходов
, определенный исходными параметрами (см. п. 3.6). Если в некотором элементе происходят фазовые переходы, то есть температура грунта равна температуре начала фазовых переходов 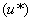 , то для этого элемента печатается число, показывающее, какая его часть находится в талом состоянии, по формату: 7XX.XX, где 7 - условная цифра, а ХХ.ХХ - процентное содержание талого грунта в элементе.
, то для этого элемента печатается число, показывающее, какая его часть находится в талом состоянии, по формату: 7XX.XX, где 7 - условная цифра, а ХХ.ХХ - процентное содержание талого грунта в элементе.
Кроме того, на печать выводятся номер элемента, через который проведен разрез, расстояние от его центра до начала координат и время на моменты печати. Для идентификации точек температурного поля двухмерная матрица окаймляется номерами элементов и значениями расстояния от их центров до начала координат.
Пример печати выходных данных приведен на рис. 5.
|
К |
1 |
0,50 м |
ВРЕМЯ Т |
6600.00 |
* |
0 ПЕРИОДА |
9 |
00.00 |
|||||
|
БЛОКИ |
ПО J |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
ПО I / |
МЕТРЫ |
2.50 |
7.50 |
12.50 |
17.50 |
22.50 |
28.00 |
28.00 |
29.50 |
30.30 |
32.00 |
||
|
1 |
0.50 |
11.80 |
11.80 |
11.80 |
11.80 |
11.80 |
11.70 |
11.57 |
10.75 |
9.08 |
8.27 |
||
|
2 |
1.50 |
6.23 |
6.23 |
6.23 |
6.23 |
6.23 |
6.18 |
5.97 |
5.28 |
4.49 |
3.68 |
||
|
3 |
2.50 |
758.48 |
758.48 |
758.48 |
758.50 |
758.48 |
757.90 |
754.66 |
740.42 |
721.60 |
709.77 |
||
|
4 |
3.50 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
-0.00 |
||
|
5 |
4.50 |
764.90 |
764.94 |
765.11 |
768.22 |
768.91 |
770.14 |
769.64 |
767.43 |
763.47 |
763.02 |
||
|
6 |
5.50 |
0.16 |
0.16 |
0.16 |
0.15 |
0.15 |
0.16 |
0.16 |
0.16 |
0.17 |
0.17 |
||
|
7 |
6.50 |
0.26 |
0.26 |
0.26 |
0.25 |
0.26 |
0.28 |
0.28 |
0.29 |
0.29 |
0.29 |
||
|
8 |
7.50 |
0.33 |
0.33 |
0.33 |
0.32 |
0.33 |
0.37 |
0.38 |
0.38 |
0.38 |
0.39 |
||
|
9 |
8.50 |
0.38 |
0.38 |
0.38 |
0.38 |
0.41 |
0.43 |
0.44 |
0.44 |
0.43 |
0.43 |
||
|
10 |
9.50 |
0.41 |
0.41 |
0.41 |
0.41 |
0.44 |
0.46 |
0.47 |
0.47 |
0.47 |
0.47 |
||
|
11 |
10.50 |
0.41 |
0.42 |
0.42 |
0.42 |
0.44 |
0.45 |
0.46 |
0.46 |
0.46 |
0.45 |
||
|
12 |
11.50 |
0.40 |
0.40 |
0.40 |
0.40 |
0.41 |
0.44 |
0.43 |
0.42 |
0.42 |
0.41 |
||
|
13 |
12.50 |
0.36 |
0.36 |
0.36 |
0.36 |
0.37 |
0.38 |
0.37 |
0.36 |
0.35 |
0.34 |
||
|
14 |
13.50 |
0.30 |
0.30 |
0.10 |
0.30 |
0.31 |
0.31 |
0.31 |
0.29 |
0.27 |
0.25 |
||
|
15 |
14.50 |
0.23 |
0.23 |
0.23 |
0.24 |
0.24 |
0.24 |
0.24 |
0.22 |
0.17 |
0.15 |
||
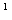 Номер элемента по К
Номер элемента по К
 Положение центра элемента (блока)
Положение центра элемента (блока)
 Время на момент печати
Время на момент печати
 Номер элемента по I
Номер элемента по I
 Положение центра элемента
Положение центра элемента
 Положение центра элемента
Положение центра элемента
 Номер элемента (блока) по I
Номер элемента (блока) по I
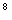
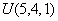 , в элементе происходит фазовый переход
, в элементе происходит фазовый переход
 Значение температуры
Значение температуры 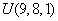
Рис. 5. Пример печати выходных данных
4.5. Подготовка данных для расчета по программе 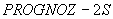
Исходные данные готовятся согласно пп. 4.2-4.3 настоящего раздела, но следующие переменные имеют постоянные значения:
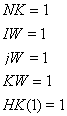
Ввод массивов 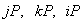 отсутствует.
отсутствует.
4.6. Подготовка данных для расчета по программе 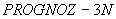
Вся исходная информация вводится с перфокарт. Данные готовятся согласно табл. 9. Все переменные, соответствующие одному порядковому номеру оператора ввода, вводятся по единому формату. Максимальное число расчетных элементов 3000, то есть 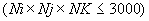 .
.
Таблица 9
|
Поряд- ковый номер опера- тора ввода |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
|
б/р |
Число элементов по направлению |
|
|
б/р |
Число элементов по направлению |
||
|
|
б/р |
Число элементов по направлению |
||
|
2 |
|
|
б/р |
Число выделенных литологических разностей |
|
|
б/р |
Число изменений шага по времени |
||
|
|
б/р |
Число интервалов времени в периоде, во время которых задаются средние значения характеристик внешней среды на верхней границе |
||
|
|
б/р |
Число зон с различными краевыми условиями на верхней границе |
||
|
|
б/р |
Число зон с различными краевыми условиями на нижней границе |
||
|
|
б/р |
Число выдаваемых на печать "разрезов" по направлению |
||
|
|
б/р |
Число выдаваемых на печать "разрезов" по направлению |
||
|
|
б/р |
Число выдаваемых на печать разрезов по направлению (см. п. 3.6) |
||
|
|
б/р |
Размер массива (см. п. 3.6) |
||
|
|
б/р |
=1, если количество теплоты измеряется в кДж |
||
|
|
б/р |
Число элементов, задающих "ступеньку" на верхней границе области исследования. Примечание. Присутствует только в алгоритме |
||
|
3 |
|
|
|
По три значения температуры, для которых задается количество незамерзшей воды, для каждой грунтовой разности в порядке их нумерации (см. табл. 4) |
|
4 |
|
|
доли ед. |
Соответствующее указанным выше температурам количество незамерзшей воды |
|
5 |
|
|
м |
Одномерный массив размерностью |
|
6 |
|
|
м |
Одномерный массив размерностью |
|
7 |
|
|
м |
Одномерный массив размерностью |
|
8 |
|
|
|
Трехмерный массив размерностью |
|
9 |
|
|
б/р |
Трехмерный массив грунта размерностью |
|
10 |
|
|
|
Двухмерный массив размерностью |
|
|
|
Двухмерный массив размерностью |
||
|
|
|
Двухмерный массив размерностью |
||
|
11 |
|
KL(Nj, Nk) |
б/р |
Двухмерный массив размерностью Примечание. В алгоритме |
|
11а |
|
S(NGR, 6) |
б/р |
Двухмерный массив размерностью NGR, 6. |
|
12 |
|
G(NSL, 6) |
Значения теплофизических характеристик грунта по выделенным слоям. Двухмерный массив размерностью (см. табл. 4) |
|
|
|
|
Плотность сухого грунта |
||
|
G(i, 2) |
|
Удельная теплоемкость сухого грунта |
||
|
G(i, 3) |
доли |
Суммарная влажность грунта |
||
|
G(i, 4) |
|
Теплопроводность мерзлого грунта |
||
|
G(i, 5) |
|
Теплопроводность талого грунта |
||
|
G(i, 6) |
|
Температура начала фазовых переходов |
||
|
13 |
6F12.2 |
SHT(i) |
ч |
Размер шага по времени с границей времени его изменения |
|
TKON |
ч |
Время окончания счета |
||
|
14 |
6F12.2 |
HPRi(iNT) |
ч |
Одномерный массив размерностью |
|
15 |
13F6.2 |
|
|
Одномерный массив размерностью |
|
TBj |
|
Простая переменная. Величина теплопотока на левой боковой границе области исследования |
||
|
TBjК |
|
Простая переменная. Величина теплопотока на правой боковой границе |
||
|
TBK |
|
Простая переменная. Величина теплопотока на ближней боковой границе |
||
|
TBKК |
|
Простая переменная. Величина теплопотока на дальней боковой границе |
||
|
16 |
|
MR(M) |
б/р |
Одномерный массив размерностью |
|
17 |
|
МК 5 |
б/р |
Одномерный массив размерностью 5. Род краевых условий соответственно на нижней, ближней, дальней, левой и правой границах |
|
18 |
|
jP(jW) |
б/р |
Одномерный массив размерностью |
|
19 |
|
KP(KW) |
б/р |
Одномерный массив размерностью |
|
20 |
|
iP(iW) |
б/р |
Одномерный массив размерностью |
4.7. Подготовка данных для расчета по программе PROGNOZ -2N
Исходные данные готовятся по табл. 9. Следующие переменные имеют постоянные значения:
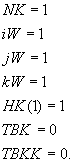
Операторы ввода с порядковыми номерами 18, 19, 20 отсутствуют. Максимальное число расчетных элементов 3000, т.е. 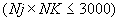 .
.
4.8. Подготовка данных для расчета по программе 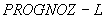
Данные готовятся согласно п. 4.7 настоящего раздела. Значение начальной температуры в фиктивных элементах (элементах, дополняющих область исследования до прямоугольной) задаются равными условному числу 99.99.
Краевые условия на верхней ступенчатой границе определяются номером зоны краевых условий на левой, верхней и правой гранях граничных элементов, формирующих верхнюю границу области исследования, и задаются массивом S размерностью 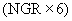 , где NGR - число граничных элементов (рис. 6).
, где NGR - число граничных элементов (рис. 6).
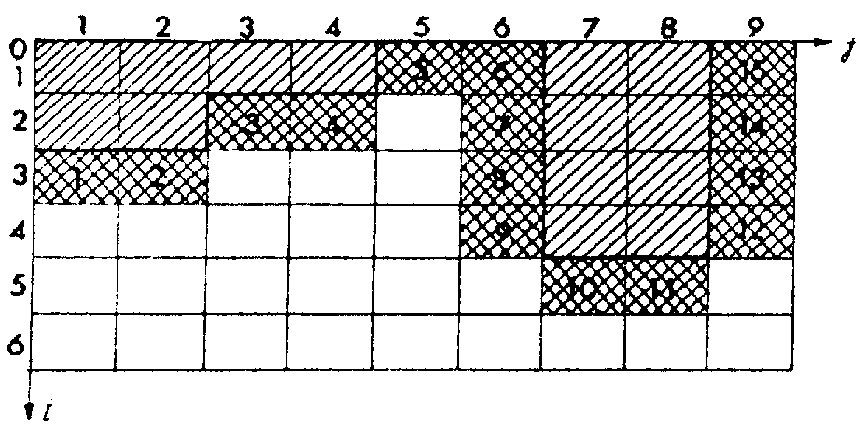
Рис. 6. Пример задания ступенчатой области решения
|
|
- |
фиктивные элементы |
|
|
|
|
|
S(d, 1) |
- |
порядковый номер элемента, |
|
S(d, 2) |
- |
координата элемента по направлению i, |
|
S(d, 3) |
- |
координата элемента по направлению |
|
S(d, 4) |
- |
номер зоны краевых условий на левой грани элемента, |
|
S(d, 5) |
- |
номер зоны краевых условий на верхней грани элемента, |
|
S(d, 6) |
- |
номер зоны краевых условий на правой грани элемента, |
По предлагаемому алгоритму не могут рассматриваться случаи, когда нижняя грань элементов, формирующих верхнюю границу области исследования, является поверхностью теплообмена с внешней средой.
Ввод двухмерного массива S осуществляется по строкам оператором ввода 11-а (см. табл. 9).
Например, на верхней границе ступенчатой области (см. рис. 6) выделено 3 зоны с различными условиями теплообмена:
|
I зона |
- |
верхние грани 1, 2, 3, 4, 10, 11 элементов; |
|
II зона |
- |
верхние грани 5, 6, 15 элементов; |
|
III зона |
- |
левые грани 3, 5, 12, 13, 14, 15 и правые грани 6, 7, 8, 9 элементов. |
Тогда массив S имеет вид:
|
|
|
|
|
|
|
|
1 |
3 |
1 |
0 |
1 |
0 |
|
2 |
3 |
2 |
0 |
1 |
0 |
|
3 |
2 |
3 |
3 |
1 |
0 |
|
4 |
2 |
4 |
0 |
1 |
0 |
|
5 |
1 |
5 |
3 |
2 |
0 |
|
6 |
1 |
6 |
0 |
2 |
3 |
|
7 |
2 |
6 |
0 |
0 |
3 |
|
8 |
3 |
6 |
0 |
0 |
3 |
|
9 |
4 |
6 |
0 |
0 |
3 |
|
10 |
5 |
7 |
0 |
1 |
0 |
|
11 |
5 |
8 |
0 |
1 |
0 |
|
12 |
4 |
9 |
3 |
0 |
0 |
|
13 |
3 |
9 |
3 |
0 |
0 |
|
14 |
2 |
9 |
3 |
0 |
0 |
|
15 |
1 |
9 |
3 |
2 |
0 |
Примечание. Приложения не приводятся. Примечание юр. бюро "Кодекс".
Текст документа сверен по:
официальное издание
Госстрой РСФСР -
М.: 1987
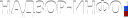
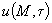
 в момент
в момент 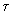 ;
;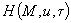
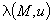
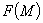
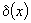
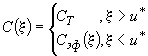
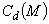
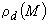
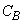
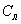
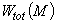
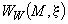
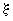 , принимается в виде
, принимается в виде 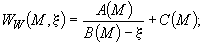
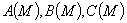
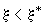 .
.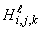
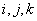 ) в момент времени
) в момент времени 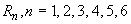
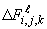
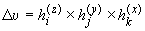 за время
за время 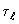 .
.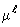
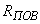
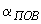
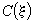
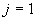
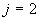 . . . . . . . . . .
. . . . . . . . . .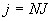
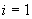
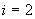
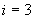
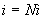
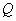
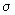
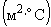
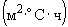 ;
;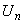
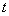 ,
, 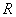 ,
, 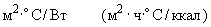
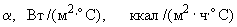
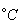
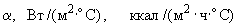
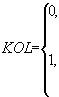
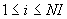 , а
, а 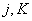 , фиксированы, внутренние источники отсутствуют;
, фиксированы, внутренние источники отсутствуют;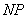
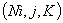 области исследования.
области исследования.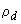
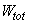
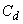
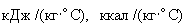 ;
;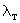
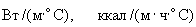 ;
;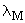
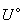
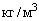
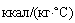
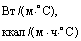
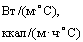
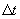
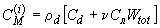
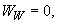
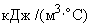 ,
, 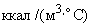 ;
;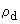
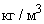 ;
;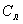
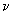
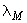
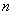
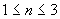 ;
;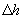
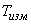
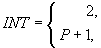
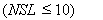
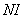
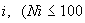 )
)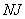
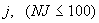
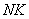
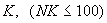
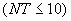
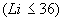
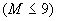
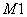
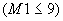
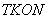
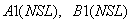
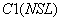
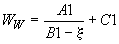
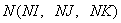
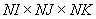 . Номера слоев грунта в соответствующих элементах (см. табл. 5)
. Номера слоев грунта в соответствующих элементах (см. табл. 5)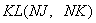
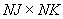 . Массив номеров зон краевых условий по элементам верхней и нижней границ (см. табл. 3)
. Массив номеров зон краевых условий по элементам верхней и нижней границ (см. табл. 3)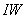
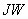
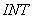
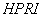 (см. п.3.6)
(см. п.3.6)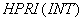
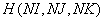
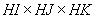 .
.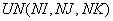
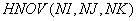
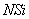
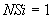 , если единица измерения количества теплоты - кДж
, если единица измерения количества теплоты - кДж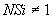 , если единица измерения количества теплоты - ккал
, если единица измерения количества теплоты - ккал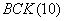
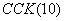
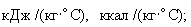
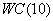
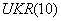
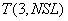
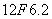
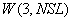
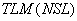
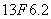
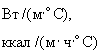
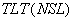
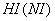
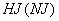
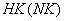
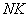 . Размер элементов по направлению
. Размер элементов по направлению 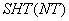
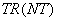
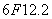
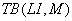
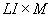 . Температура внешней среды на верхней границе области исследования при периодическом ее изменении по времени и зонам краевых условий в порядке их нумерации (см. табл. 2)
. Температура внешней среды на верхней границе области исследования при периодическом ее изменении по времени и зонам краевых условий в порядке их нумерации (см. табл. 2)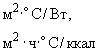
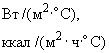
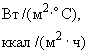
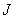 , задающие “разрезы”, для которых выводится на печать распределение температур (см. п.3.6). Если печать не нужна, то
, задающие “разрезы”, для которых выводится на печать распределение температур (см. п.3.6). Если печать не нужна, то 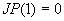
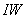 . Номера элементов по направлению
. Номера элементов по направлению 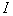 , задающие “разрезы”, для которых выводится на печать распределение температур. Если печать не нужна, то
, задающие “разрезы”, для которых выводится на печать распределение температур. Если печать не нужна, то 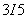
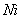
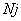
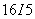
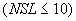
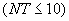
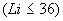
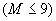
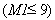
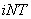
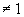 , если количество теплоты измеряется в ккал
, если количество теплоты измеряется в ккал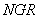
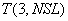
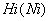
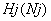
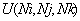
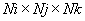 . Начальная температура грунта по элементам (см. табл. 1).
. Начальная температура грунта по элементам (см. табл. 1).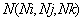
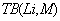
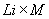 . Температура внешней среды на верхней границе области исследования при периодическом ее изменении по времени и зонам краевых условий в порядке их нумерации (см. табл. 2)
. Температура внешней среды на верхней границе области исследования при периодическом ее изменении по времени и зонам краевых условий в порядке их нумерации (см. табл. 2)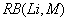
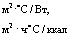
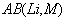
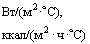
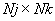 . Массив номеров зон краевых условий по элементам верхней и нижней границ (см. табл. 3)
. Массив номеров зон краевых условий по элементам верхней и нижней границ (см. табл. 3)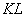 номер зоны краевых условий по элементам верхней границы задается равным 1
номер зоны краевых условий по элементам верхней границы задается равным 1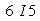
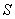 присутствует только в алгоритме
присутствует только в алгоритме 
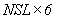
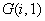
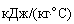
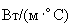
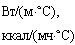
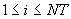
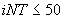 . Задает интервалы выдачи на печать температуры грунта (час) (см. п. 3.6)
. Задает интервалы выдачи на печать температуры грунта (час) (см. п. 3.6)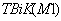
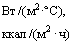
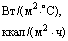
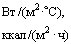
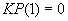 (см. п. 3.6)
(см. п. 3.6)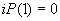 (см. п. 3.6)
(см. п. 3.6)

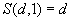 ;
;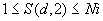 ;
;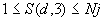 ;
;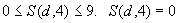 , если эта грань не является поверхностью теплообмена с внешней средой;
, если эта грань не является поверхностью теплообмена с внешней средой;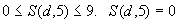 , если эта грань не является поверхностью теплообмена с внешней средой;
, если эта грань не является поверхностью теплообмена с внешней средой;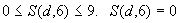 , если эта грань не является поверхностью теплообмена с внешней средой.
, если эта грань не является поверхностью теплообмена с внешней средой.